معرفی انواع رگرسیون و کاربردهای آن ها

کسب‌وکارها می‌توانند از ابزارهای آماری مانند تحلیل انواع رگرسیون برای کمک به ارزیابی رابطه بین دو متغیر استفاده کنند.

ممکن است شما بخواهید از تجزیه و تحلیل رگرسیون برای تعیین تاثیر افزایش قیمت یک محصول بر تعداد افراد خریدار آن محصول یا تاثیر آب و هوا بر تصمیمات خرید مخاطبان، استفاده کنید.

درک تحلیل رگرسیون می‌تواند به شما کمک کند تا تصمیمات تجاری موثرتری برای شرکتی که در آن کار می‌کنید یا تیم خود بگیرید.

در این مقاله، تحلیل انواع رگرسیون را بررسی می‌کنیم، کاربرد و مزایای آن‌ها را ارائه می‌دهیم و توضیح می‌دهیم که چگونه تحلیل رگرسیون را برای بهینه‌سازی فرآیندهای تصمیم‌گیری حرفه‌ای انجام دهیم.

1# تحلیل رگرسیون چیست؟

تحلیل رگرسیون، در مدل‌سازی آماری، راهی برای مرتب‌سازی ریاضی مجموعه‌ای از متغیرها است و ما از آن برای تعیین این که کدام متغیرها تأثیر دارند و چگونه با یکدیگر ارتباط دارند، استفاده می‌کنیم.

به‌عبارت دیگر، تجزیه و تحلیل رگرسیون به ما کمک می‌کند تا مشخص کنیم کدام عوامل بیشتر اهمیت دارند و کدامیک را می‌توانیم، نادیده بگیریم.

هم‌چنین به ما کمک می‌کند تا تعیین کنیم کدام عوامل با یکدیگر تعامل دارند.

علاوه بر این و مهمتر از همه، به ما کمک می‌کند تا بفهمیم که در مورد همه عواملی که بررسی کرده‌ایم، چقدر مطمئن هستیم.

از انواع تجزیه و تحلیل رگرسیون در سرمایه‌گذاری، مالی، فروش، بازاریابی، علوم، ریاضیات و غیره استفاده می‌کنیم.

این تحلیل سعی می‌کند، تعیین کند که یک متغیر وابسته چقدر با یک سری متغیرهای دیگر مرتبط است و ما معمولا از آن‌ها به‌عنوان متغیرهای مستقل یاد می‌کنیم.

متغیر وابسته همانی است که روی آن تمرکز می‌کنیم.

به بیان ساده، ما می‌خواهیم بدانیم که آیا این متغیر تحت تأثیر قرار گرفته است یا خیر؟ و اگر چنین است چه مقدار و تحت چه چیزی قرار گرفته است.

متغیرهای مستقل عواملی هستند که ممکن است بر متغیر وابسته تأثیر بگذارند یا نگذارند.

متغیرهای وابسته تأثیر را دریافت می‌کنند، درحالی‌که متغیرهای مستقل تأثیر را ارائه می‌دهند.

2# تاریخچه تحلیل رگرسیون

ریاضیدان فرانسوی آدرین ماری لژاندر (1752-1833) اولین شکل رگرسیون را که ما از آن می شناسیم در سال 1805 منتشر کرد.

ریاضیدان آلمانی یوهان کارل فردریش گاوس (1777-1855) نیز قطعه‌ای را در سال 1809 منتشر کرد.

هر دو ریاضیدان در مورد روش حداقل مربعات نوشتند.

روش حداقل مربعات یک رویکرد استاندارد در تحلیل رگرسیونی است که تعداد معادلات بیشتر از مجهولات باشد.

گاوس و لژاندر این روش را برای مسئله یافتن مدارهای اجرام مختلف آسمانی به‌کار بردند.

آن‌ها عمدتاً بر مدارهای دنباله‌دار به دور خورشید تمرکز کردند.

در سال 1821، گاوس توسعه دیگری را برای نظریه حداقل مربعات در سال 1821 منتشر کرد.

او نسخه‌ای از آن‌چه که ما آن‌ را قضیه گاوس-مارکف می‌نامیم، ارائه داد.

سر فرانسیس گالتون (1922-1911)، آماردان بریتانیایی، اصطلاح تحلیل رگرسیون را در قرن نوزدهم ابداع کرد.

او این اصطلاح را هنگام توصیف قد افراد در طول نسل‌ها به‌کار برد.

مطالعه او نشان داد که قد نوادگان اجداد بسیار بلند قد، در نسل‌های بعدی به سمت میانگین معمولی حرکت می‌کند.

در واقع، ما این را رگرسیون به سمت میانگین می‌نامیم.

گالتون معتقد بود که رگرسیون تنها زمانی قابل استفاده است که از آن برای توصیف پدیده بیولوژیکی که کشف کرده بود، استفاده کند.

با این حال، کارل پیرسون (1857-1936) و جورج اودنی یول (1871-1951) کار او را به یک زمینه آماری عمومی‌تر گسترش دادند.

در اواسط قرن بیستم، اقتصاددانان از ماشین حساب‌های میز الکترومکانیکی برای محاسبات تحلیل رگرسیون استفاده می‌کردند.

تا سال 1970، ممکن بود، بیست و چهار ساعت طول بکشد تا نتیجه یک رگرسیون به‌دست آید.

3# نحوه انجام مطالعه انواع رگرسیون

به‌دلیل پیچیدگی بسیار زیاد، اغلب مدل‌های تحلیل رگرسیون را برنامه‌های صفحه گسترده کامپیوتری یا ماشین حساب‌های تخصصی، اجرا می‌کنند.

چه شما مسئول تهیه این نوع مطالعه باشید و چه از نرم افزار استفاده کنید، درک فرآیند استفاده تحلیلگران داده مفید است:

• یک مطالعه تجزیه و تحلیل رگرسیون را سازماندهی کنید: نیاز تحقیق خود را تعیین کنید، اگر مثلا پیش‌بینی فروش باشد، بودجه بسازید یا یک استراتژی تبلیغاتی جدید ایجاد کنید.
• تمرکز را محدود کنید: در مورد آن‌چه تیم برای دستیابی به بهترین داده‌های ممکن به‌دنبال آن است، تمرکز کنید.
  به‌عنوان مثال، تعیین این‌که آیا چترهای بیشتری در هنگام بارندگی به فروش می‌رسند یا نه، مهم‌تر از تعیین تعداد فروش در هنگام هوای بد است.
• داده‌ها را وارد کنید: تمام نقاط نمودار داده را برای متغیرهای X و Y با حجم نمونه و مشاهدات به اندازه کافی بزرگ، اضافه کنید.
• تجزیه و تحلیل نتایج: یک خط از وسط تمام نقاط داده رسم کنید تا همبستگی بین متغیرها را ببینید.
• اصطلاح خطا را در نظر بگیرید: تحلیل رگرسیون یک تخمین است و یک پیش بینی کامل نیست.
  هر چه عبارت خطا بیشتر باشد، خط رگرسیون همبستگی، قطعیت کمتری دارد.
• ایجاد یک گزارش و استراتژی: یافته‌های خود را ثبت کنید و آن‌ها را در طرح، پیش‌بینی یا بودجه کسب و کار خود اعمال کنید.

4# اهمیت تحلیل رگرسیون

اهمیت تحلیل رگرسیون به‌شرح زیر است:

1-4# شناسایی رابطه

تحلیل رگرسیون به شناسایی و کمی کردن رابطه بین یک متغیر وابسته و یک یا چند متغیر مستقل کمک می‌کند و به ما امکان می‌دهد تا تعیین کنیم که چگونه تغییرات در متغیرهای مستقل بر متغیر وابسته تأثیر می‌گذارند و وجود این اطلاعات برای تصمیم‌گیری، برنامه‌ریزی و پیش‌بینی حیاتی است.

2-4# پیش‌بینی

تحلیل رگرسیون ما را قادر می‌سازد تا براساس روابط شناسایی شده پیش‌بینی را انجام دهیم.

با تخمین مقادیر متغیر وابسته با استفاده از مقادیر شناخته‌شده متغیرهای مستقل، مدل‌های رگرسیون می‌توانند بینش ارزشمندی را در مورد نتایج آتی ارائه دهند.

این امر به‌ویژه در تجارت و اقتصاد، امور مالی و سایر زمینه‌هایی که پیش‌بینی برای برنامه‌ریزی و توسعه استراتژی در آن‌ها حیاتی است، مفید می‌باشد.

3-4# ارزیابی علیت

در حالی که همبستگی دلالت بر علیت ندارد، تحلیل رگرسیون چارچوبی برای ارزیابی علیت با در‌ نظر گرفتن جهت و قدرت رابطه بین متغیرها فراهم می‌کند و این به محققان اجازه می‌دهد تا عوامل دیگر را کنترل کنند و تأثیر یک متغیر مستقل خاص را بر متغیر وابسته ارزیابی کنند.

این کار به تعیین تأثیر علیت و شناسایی عوامل مهمی که بر نتایج تأثیر می‌گذارند، کمک می‌نماید.

4-4# ساخت مدل و انتخاب متغیر

تحلیل رگرسیون با تعیین مناسب‌ترین شکل عملکردی رابطه بین متغیرها به ساخت مدل کمک می‌نماید تا محققان بتوانند متغیرهای مستقل مرتبط را انتخاب و متغیرهای نامربوط را حذف کنند، پیچیدگی را کاهش دهند و دقت مدل را بهبود بخشند.

این فرآیند برای ایجاد مدل‌های قوی و قابل تفسیر بسیار مهم است.

5-4# آزمون فرضیه

تحلیل رگرسیون چارچوبی آماری برای آزمون فرضیه‌ها فراهم می‌کند و محققان می‌توانند با آزمایش اهمیت ضرایب فردی، برازش کلی مدل را ارزیابی نمایند و تعیین کنند که آیا رابطه بین متغیرها از نظر آماری معنادار است یا خیر؟

که این‌مورد امکان تجزیه و تحلیل دقیق و اعتبار‌سنجی فرضیه‌های تحقیق را فراهم می‌نماید.

6-4# ارزیابی خط‌ مشی و تصمیم‌گیری

انواع رگرسیون نقش حیاتی در ارزیابی سیاست و فرآیندهای تصمیم‌گیری ایفا می‌کنند.

با تجزیه و تحلیل داده‌های تاریخی، محققان می‌توانند اثربخشی مداخلات سیاستی را ارزیابی کنند و عوامل کلیدی مؤثر در نتایج معین را شناسایی کنند.

این اطلاعات به سیاستگذاران کمک می‌کند تا تصمیمات آگاهانه بگیرند، منابع را به‌طور موثر تخصیص دهند و اجرای سیاست را بهینه کنند.

7-4# ارزیابی و کنترل ریسک

تحلیل رگرسیون را می‌توان برای اهداف ارزیابی ریسک و کنترل آن استفاده کرد.

با تجزیه و تحلیل داده‌های تاریخی، سازمان‌ها می‌توانند عوامل خطر را شناسایی کنند و مدل‌هایی را توسعه دهند که احتمال برخی از نتایج، مانند پیش‌فرض، تصادف یا شکست را پیش‌بینی می‌کنند.

این امر مدیریت ریسک فعال را قادر می سازد تا اقدامات پیشگیرانه را انجام دهند و خطرات بالقوه را کاهش دهند.

5# انواع رگرسیون

انواع رگرسیون به‌شرح زیر است:

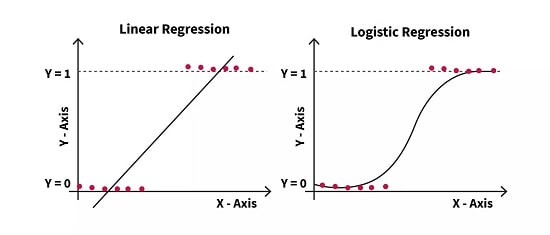
1-5# رگرسیون خطی

رگرسیون خطی اساسی‌ترین و پرکاربردترین شکل تحلیل رگرسیون است و رابطه خطی بین یک متغیر وابسته و یک یا چند متغیر مستقل را مدل می‌کند و هدف یافتن بهترین خطی است که مجموع اختلاف مجذور بین مقادیر مشاهده شده و پیش‌بینی شده را به حداقل برساند.

2-5# رگرسیون چندگانه

رگرسیون چندگانه با ترکیب دو یا چند متغیر مستقل برای پیش‌بینی متغیر وابسته، رگرسیون خطی را گسترش می‌دهد و این امکان را برای بررسی اثرات همزمان چند پیش‌بینی کننده بر روی متغیر نتیجه فراهم می‌نماید.

3-5# رگرسیون چند جمله‌ای

رگرسیون چند جمله‌ای، روابط غیر‌خطی بین متغیرها را با افزودن عبارت‌های چند جمله‌ای (مثلاً مجذور یا مکعب) به معادله رگرسیون مدل می‌کند و می‌تواند الگوهای منحنی یا غیرخطی را در داده‌ها ثبت نماید.

4-5# رگرسیون لجستیک

رگرسیون لجستیک زمانی استفاده می‌شود که متغیر وابسته باینری باشد.

این نوع رگرسیون احتمال وقوع یک رویداد یا نتیجه خاص را براساس متغیرهای مستقل مدل می‌کند.

رگرسیون لجستیک با تخمین ضرایب با استفاده از تابع لجستیک ترکیب خطی پیش‌بینی کننده‌ها را به یک احتمال تبدیل می‌کند.

5-5# رگرسیون ریج (Ridge) و رگرسیون لاسو (Lasso)

رگرسیون ریج و رگرسیون لاسو تکنیک‌هایی هستند که برای پرداختن به چند خطی (همبستگی زیاد بین متغیرهای مستقل) و انتخاب متغیر استفاده می‌شوند.

هر دو روش یک عبارت جریمه را به معادله رگرسیون معرفی می‌کنند تا متغیرهای کم اهمیت‌تر را کوچک یا حذف نمایند.

رگرسیون ریج از منظم‌سازی L2 و رگرسیون لاسو از منظم‌سازی L1 استفاده می‌کنند.

6-5# رگرسیون سری زمانی

رگرسیون سری زمانی، رابطه بین متغیر وابسته و متغیرهای مستقل را هنگامی‌که داده‌ها در طول زمان جمع‌آوری می‌شوند، تجزیه و تحلیل می‌کند.

این نوع، خود‌همبستگی و روندها در داده‌ها را محاسبه می‌کند و در پیش‌بینی و مطالعه روابط زمانی استفاده می‌شود.

7-5# رگرسیون غیر خطی

زمانی که رابطه بین متغیر وابسته و متغیر مستقل خطی نباشد از مدل‌های رگرسیون غیرخطی استفاده می‌شود.

این مدل‌ها می‌توانند اشکال عملکردی مختلفی داشته باشند و به تکنیک‌های تخمینی متفاوت از روش‌های مورد استفاده در رگرسیون خطی نیاز دارند.

8-5# رگرسیون پواسون

رگرسیون پواسون زمانی استفاده می‌شود که متغیر وابسته، داده‌های شمارش را نشان دهد.

با فرض توزیع پواسون برای متغیر وابسته، این نوع رگرسیون رابطه بین متغیرهای مستقل و تعداد مورد انتظار را مدل می‌نماید.

9-5# مدل‌های خطی تعمیم‌یافته (GLM)

GLM ها یک کلاس انعطاف‌پذیر از مدل‌های رگرسیونی هستند که چارچوب رگرسیون خطی را برای مدیریت انواع مختلف متغیرهای وابسته، ازجمله متغیرهای باینری، شمارش و پیوسته گسترش می‌دهند.

GLM ها دارای توزیع‌های احتمالی مختلف و توابع پیوند هستند.

6# فرمول‌های انواع رگرسیون

تحلیل انواع رگرسیون شامل تخمین پارامترهای یک مدل رگرسیونی برای توصیف رابطه بین متغیر وابسته (Y) و یک یا چند متغیر مستقل (X) است.

در اینجا فرمول‌های اساسی رگرسیون خطی، رگرسیون چندگانه و رگرسیون لجستیک آورده شده است:

1-6# رگرسیون خطی

مدل رگرسیون خطی ساده:

مدل رگرسیون خطی چندگانه:

در هر دو فرمول:

• Y نشان‌دهنده متغیر وابسته (متغیر پاسخ) است.
• X نشان‌دهنده متغیر(های) مستقل (متغیرهای پیش‌بینی کننده) است.
• β0 ،β1 ،β2 ،… ،βn ضرایب یا پارامترهایی هستند که باید تخمین زده شوند.
• ε نشان‌دهنده عبارت خطا یا باقیمانده (تفاوت بین مقادیر مشاهده‌شده و پیش‌بینی‌شده) است.

2-6# رگرسیون چندگانه

رگرسیون چندگانه مفهوم رگرسیون خطی ساده را با گنجاندن چندین متغیر مستقل گسترش می‌دهد.

مدل رگرسیون چندگانه:

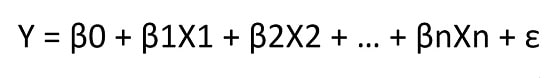
فرمول‌ها مشابه فرمول‌های رگرسیون خطی هستند و متغیرهای مستقل بیشتری اضافه می‌شوند.

3-6# رگرسیون لجستیک

رگرسیون لجستیک زمانی استفاده می‌شود که متغیر وابسته باینری باشد.

مدل رگرسیون لجستیک یک تابع لجستیک یا سیگموئید را برای ترکیب خطی متغیرهای مستقل اعمال می‌کند.

مدل رگرسیون لجستیک:

در فرمول:

• p نشان‌دهنده احتمال وقوع رویداد است (به‌عنوان مثال، احتمال موفقیت یا تعلق به یک دسته خاص).
• β0 ،β1 ،β2 ،… ،βn ضرایب یا پارامترهایی هستند که باید تخمین زده شوند.
• X1 ،X2 ،… ،Xn نشان‌دهنده متغیرهای مستقل هستند.
• e پایه لگاریتم طبیعی است.

تابع لجستیک تضمین می‌کند که احتمالات پیش‌بینی‌شده بین 0 و 1 قرار داشته باشند و امکان طبقه‌بندی باینری را فراهم می‌کند.

7# کاربردهای انواع رگرسیون

در ادامه برخی از کاربردهای رایج انواع رگرسیون آورده شده است:

1-7# پیش‌بینی اقتصادی

تحلیل رگرسیون اغلب در علم اقتصاد برای پیش‌بینی متغیرهایی مانند رشد تولید ناخالص داخلی، نرخ تورم یا عملکرد بازار سهام استفاده می‌شود.

با تجزیه و تحلیل داده‌های تاریخی و شناسایی روابط زیربنایی، اقتصاددانان می‌توانند پیش بینی‌هایی در مورد شرایط اقتصادی آینده داشته باشند.

2-7# تجزیه و تحلیل مالی

تجزیه و تحلیل رگرسیون نقش مهمی در تجزیه و تحلیل مالی از جمله پیش بینی قیمت سهام یا ارزیابی تاثیر عوامل مالی بر عملکرد شرکت ایفا می‌نماید و این به تحلیلگران کمک می‌کند تا بفهمند چگونه متغیرهایی مانند نرخ بهره، درآمد شرکت یا شاخص‌های بازار بر نتایج مالی تأثیر می‌گذارند.

3-7# تحقیقات بازاریابی

تجزیه و تحلیل رگرسیون به بازاریابان کمک می‌کند تا رفتار مصرف‌کننده را درک کنند و تصمیمات مبتنی بر داده اتخاذ نمایند.

در نتیجه می‌توان از آن برای پیش‌بینی فروش براساس هزینه‌های تبلیغاتی، استراتژی‌های قیمت‌گذاری یا متغیرهای جمعیت شناختی استفاده کرد.

مدل‌های رگرسیون بینش‌هایی را ارائه می‌دهند که تلاش‌های بازاریابی مؤثرترین هستند و به بهینه‌سازی کمپین‌های بازاریابی کمک می‌کنند.

4-7# علوم بهداشتی

تحلیل رگرسیون به‌طور گسترده در تحقیقات پزشکی و مطالعات بهداشت عمومی استفاده می‌شود و به بررسی رابطه بین عوامل خطر و پیامدهای سلامتی، مانند تأثیر سیگار بر سرطان ریه یا رابطه بین رژیم غذایی و بیماری قلبی کمک می‌کند.

تجزیه و تحلیل رگرسیون هم‌چنین به پیش‌بینی نتایج سلامت براساس عوامل مختلف مانند سن، نشانگرهای ژنتیکی یا انتخاب سبک زندگی کمک می‌نماید.

5-7# مطالعات محیطی

تحلیل رگرسیون به درک و پیش‌بینی پدیده‌های محیطی کمک می‌کند و می‌توان از آن برای تجزیه و تحلیل تأثیر عواملی مانند دما، سطوح آلودگی یا الگوهای کاربری زمین بر پدیده‌هایی مانند تنوع گونه‌ها، کیفیت آب یا تغییرات آب و هوایی استفاده کرد.

6-7# تجزیه و تحلیل ورزشی

تجزیه و تحلیل رگرسیون به‌طور فزآینده‌ای در تجزیه و تحلیل ورزشی برای به‌دست آوردن بینش در مورد عملکرد بازیکن، استراتژی‌های تیم و نتایج بازی استفاده می‌شود.

هم‌چنین به تجزیه و تحلیل رابطه بین عوامل مختلف مانند آمار بازیکنان، استراتژی‌های مربیگری یا شرایط محیطی و تأثیر آن‌ها بر نتایج بازی کمک می‌کند.

8# مزایا و معایب تحلیل رگرسیون

1-8# مزایا

• معیار کمی از رابطه بین متغیرها را ارائه می‌دهد.
• به پیش‌بینی نتایج براساس داده‌های تاریخی کمک می‌کند.
• اهمیت متغیرهای مستقل را بر روی متغیر وابسته شناسایی و اندازه‌گیری می‌کند.
• تخمین‌هایی از ضرایب ارائه می‌کند که قدرت و جهت رابطه بین متغیرها را نشان می‌دهد.
• به آزمون فرضیه برای تعیین اهمیت آماری رابطه اجازه می‌دهد.
• می‌تواند متغیرهای پیوسته و طبقه‌ای را مدیریت کند.
• با استفاده از نمودارهای پراکندگی و خطوط رگرسیون، نمایش بصری رابطه را ارائه می‌دهد.
• بینشی در مورد اثرات حاشیه‌ای متغیرهای مستقل بر متغیر وابسته ارائه می‌دهد.

2-8# معایب

• یک رابطه خطی بین متغیرها را فرض می‌کند که ممکن است همیشه درست نباشد.
• برای تولید نتایج قابل اعتماد به حجم نمونه بزرگ نیاز دارد.
• هیچ تابع چند خطی را فرض نمی‌کند، به این معنی که متغیرهای مستقل نباید همبستگی زیادی با یکدیگر داشته باشند.
• عدم وجود نقاط پرت یا تأثیرگذار را فرض می‌کند.
• می‌تواند به گنجاندن یا حذف متغیرهای خاص حساس باشد که منجر به نتایج متفاوتی شود.
• تجزیه و تحلیل رگرسیون از نظر آماری نشان می‌دهد که آیا دو عنصر با یکدیگر مرتبط هستند یا نه؟
• اگرچه در‌ نظر گرفتن شهود انسان همراه با داده‌ها نیز مهم است. مدیران ماهر و شرکت‌های هوشمند می‌توانند به نتایج تحلیل رگرسیون نگاه کنند و آن‌ها را با خرد تجاری، تجربه و درک موقعیت خود مقایسه کنند.

اگر به دنبال یاد گرفتن مهارت بیشتر و افزایش درآمد هستید،

برای دریافت آموزش های رایگان مرتبط با حوزه علاقه‌مندی خود فقط کافیه فرم رو تکمیل کنید.

نظرتون درباره این مقاله چیه؟
ما رو راهنمایی کنید تا اون رو کامل تر کنیم و نواقصش رو رفع کنیم.
توی بخش دیدگاه ها منتظر پیشنهادهای فوق العاده شما هستیم.