آشنایی با روش المان محدود

روش المان محدود (FEM) سنگ بنای حرفه ای برخی محاسبات است.

ممکن است ابتدا این روش کمی سخت و گیج کننده باشد و ظاهرا کار ترسناکی به نظر برسد؛
زیرا از آن به عنوان “شکنجه های ریاضی” یاد می شود.

برای شروع فقط باید بدانید که چگونه مدل های خود را پشتیبانی کرده و مش بندی کنید، چه بارهایی را بارگذاری و چگونه نتایج را تحلیل و تفسیر نمایید.

اکنون ما این راهنما را برای کمک به شما در شروع FEM آماده کرده ایم تا
با حل یک معادله به زبانی ساده با مبانی روش المان محدود آشنا شوید.

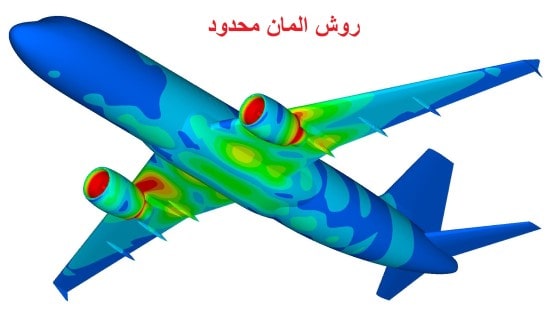
1# تعریف روش المان محدود (Finite Element Method)

راه حل های صریح و بسته برای معادلات دیفرانسیل جزئی (PDE) به ندرت در دسترس هستند.

روش المان محدود (FEM) که به آن تحلیل المان محدود (finite element analysis) یا FEA نیز گفته می شود،
روشی برای حل عددی معادلات دیفرانسیل جزئی است.

حداقل به دو دلیل مهم است:

1. روش المان محدود قادر است PDE ها را تقریباً در هر منطقه ای که خودسرانه شکل گرفته حل کند.
2. این روش برای استفاده در یک گروه وسیع از PDE مناسب است.

در حالی که تقریباً همیشه می توان روش های بهتری را برای یک PDE خاص در یک منطقه خاص تصور کرد،
روش المان محدود برای یک گروه وسیع از PDE ها بسیار خوب عمل می کند.

این یک روش ریاضی برای تجزیه و تحلیل نقاط تنش یا شکست است.

ساختار یا سیستم به زیرسازی هایی موسوم به “المان های محدود” تقسیم می شود.

المان های محدود و روابط متقابل آن ها را می توان به منظور شناسایی یا طراحی مجدد ارزیابی کرد.

هم چنین این روش، تکنیکی برای مدل سازی یک ساختار پیچیده است.

هنگامی که مدل ریاضی تحت بار شناخته شده قرار می گیرد، می توان جا به جایی ساختار را تعیین کرد.

روش المان محدود با نتایج قابل توجهی در مدل سازی چندین کاربرد مکانیکی مربوط به هوا فضا و مهندسی عمران آغاز شد.

یکی از جالب ترین چشم اندازها کاربرد آن در حل مشکلاتی از جمله موارد زیر است:

• تعامل مایع با سیستم
• ترمومکانیک
• ترموشیمی
• مشکلات حرارتی شیمی مکانیکی
• بیومکانیک
• مهندسی پزشکی
• پیزوالکتریک
• فروالکتریک
• الکترومغناطیس

2# تاریخچه روش المان محدود

روش المان محدود از نیاز به حل مشکلات کشش پیچیده و تجزیه و تحلیل ساختاری در مهندسی عمران و هوانوردی نشأت گرفته است.

پیشرفت آن را می توان در اثری دنبال کرد با نام گسسته سازی که الکساندر هرنیکوف (1941) و ریچارد کورانت (1942) پایه گذاری کرده اند.

توسعه روش المان محدود به طور جدی در اواخر دهه 1950 برای چارچوب هوا و تجزیه و تحلیل سازه آغاز شد و
با استفاده از جان آرگیریس در دانشگاه اشتوتگارت و در سال 1960 در برکلی برای استفاده از کار ری دبلیو کلاف جمع آوری شد.

در اواخر دهه 1950، مفاهیم اصلی ماتریس سختی و مونتاژ عناصر اساساً همان طور که امروزه استفاده می شود وجود داشتند.

ناسا درخواست های پیشنهادی برای توسعه نرم افزار اجزای محدود NASTRAN در سال 1965 را صادر کرده است.

3# مولفه های روش المان محدود

آن چه برای تجزیه و تحلیل عناصر محدود مورد نیاز است و
برای حل معادلات دیفرانسیل جزئی با روش المان محدود به کار می گیریم، تنها سه مولفه به صورت زیر است:

• یک نمایش گسسته از یک ناحیه، به عنوان مثال یک المان
• یک معادله دیفرانسیل جزئی
• شرایط مرزی که معادله را با ناحیه پیوند می دهد

برای این کار به معادلات دیفرانسیل جزئی و شرایط مرزی آن ها می پردازد.

مش های عناصر محدود را می توان با ToElementMesh تولید کرد.

4# مراحل مختلف روش المان محدود

در ادامه، شرح مختصری از مکانیسم FEM آورده شده است.

برای به تصویر کشیدن مراحل مختلف مربوط به FEA، یک مسئله ساده را در نظر بگیرید.

1-4# شکل ضعیف

یکی از اولین مراحل در روش المان محدود شناسایی PDE مرتبط با پدیده فیزیکی است.

PDE (یا فرم دیفرانسیل) به عنوان فرم قوی و فرم انتگرال به عنوان فرم ضعیف شناخته می شود.

همانند تصویر زیر یک PDE ساده را در نظر بگیرید.

معادله در هر دو طرف در یک تابع آزمایشی v(x) ضرب می شود و با دامنه ترکیب می شود.

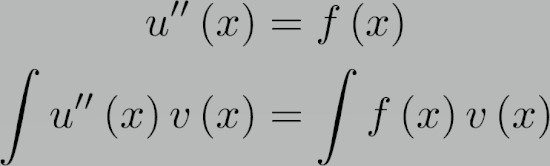
حالا با استفاده از انتگرال گیری سمت چپ معادله، می توان آن را به فرم زیر کاهش داد.

‍

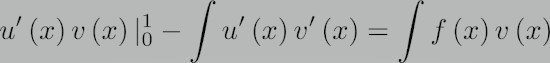
همان طور که مشاهده می شود، درجه پیوستگی در معادله تابع ناشناخته u(x) یکی کمتر می شود.

معادله دیفرانسیلی اولیه برای u(x) نیاز به دو مرتبه مشتق پذیری این تابع داشت،
در حالی که با استفاده از معادله انتگرالی به یک مرتبه مشتق پذیری کاهش یافته است.

در مورد توابع چند بعدی نیز همین مسئله وجود دارد؛ اما مشتقات با گرادیان و دیورژانس جایگزین می شوند.

بدون ورود به ریاضیات، قضیه نمایش Riesz می تواند ثابت کند که
برای محاسبه تابع u(x) با استفاده از انتگرال و به شکل دیفرانسیلی یک راه حل یکتا وجود دارد.

همچنین اگر تابع f(x) هموار باشد نتیجه می دهد که قطعا x(x) هموار است.

2-4# گسسته سازی

پس از تضعیف فرم انتگرال، مرحله بعدی روش المان محدود، گسسته سازی فرم ضعیف است.

فرم انتگرال باید به صورت عددی حل شود و از این رو ادغام به یک جمع تبدیل می شود که
به صورت عددی قابل محاسبه است.

یکی از اهداف اصلی گسسته سازی نیز تبدیل فرم انتگرال به مجموعه ای از معادلات ماتریس است که
با استفاده از نظریه های معروف جبر ماتریس قابل حل است.

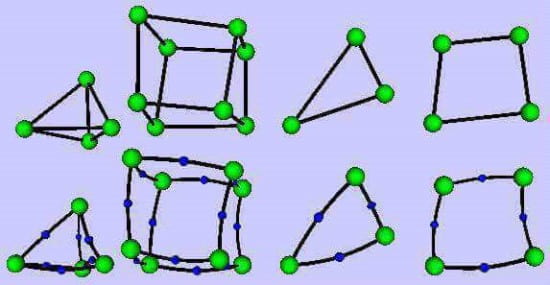
همان طور که در شکل نشان داده شده است، دامنه به قطعات کوچک معروف به “المان” تقسیم شده و
نقطه گوشه هر عنصر به عنوان “گره” شناخته می شود.

عملکرد ناشناخته u(x) در نقاط گره ای محاسبه می شود.

برای درون یابی توابع برای هر المان، با استفاده از مقادیر گره ای تعریف می شود؛
بنابراین عملکرد ناشناخته u(x) را می توان به شکل زیر کاهش داد:

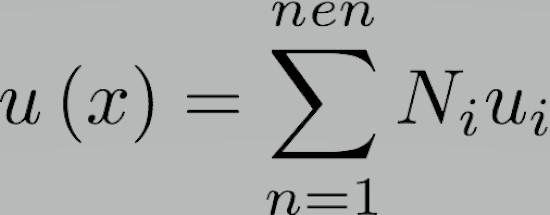
nen تعداد گره های موجود در عنصر است، Ni و ui به ترتیب تابع درون یابی و ناشناخته های مرتبط با گره i هستند.

به همین ترتیب، می توان برای سایر توابع v(x) و f(x) موجود در فرم ضعیف، از درون یابی استفاده کرد؛
بنابراین فرم ضعیف می تواند به صورت زیر باشد:

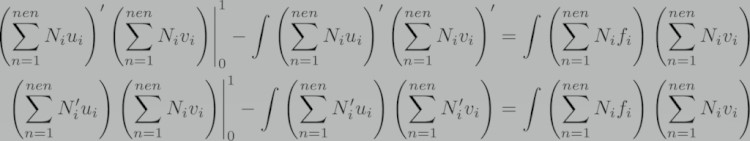
طرح های جمع بندی را می توان به شکل ماتریسی تبدیل کرد و به صورت زیر نوشت:

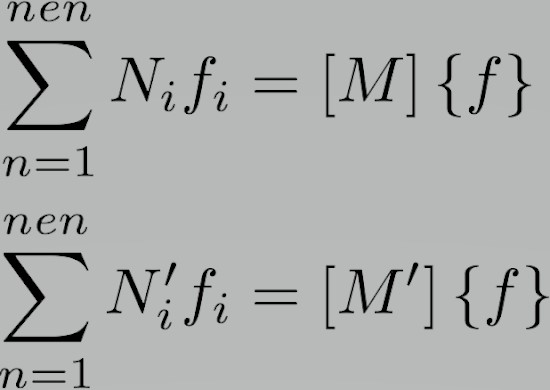
فرم ضعیف اکنون می تواند به فرم ماتریسی کاهش یابد:

[K]{u}={f}

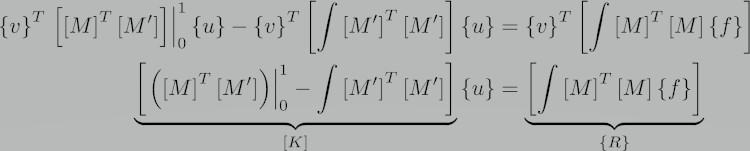
در بالا توجه داشته باشید که تابع آزمایشی قبلی v(x) که ضرب شده است دیگر در معادله ماتریس حاصل وجود ندارد.

در این جا [K] به عنوان ماتریس سختی شناخته می شود، {u} بردار مجهولات گره ای است و {R} بردار باقیمانده است.

به علاوه با استفاده از طرح های یکپارچه سازی عددی مانند کوارتر Gauss یا Newton-Cote، ادغام ها در فرم ضعیف که باعث ایجاد سختی مماس و بردار باقیمانده می شوند به راحتی کنترل می شوند.