به منظور تجزیه و تحلیل اطلاعات نیاز است که داده ها بر اساس یک نظم منطقی طبقه بندی شوند تا به این صورت معنادار و قابل تفسیر باشند و یکی از راه های طبقه بندی اطلاعات این است که
داده ها را در یک جدولی به نام جدول توزیع فراوانی گردآوری کنیم.
این روش جمع آوری داده ها در بسیاری از حوزه های فنی و آماری کمک کننده بوده و روشی بنیادی برای بررسی داده هاست.
در این مقاله با ما همراه باشید تا شما را به طور کامل با توزیع فراوانی آشنا کنیم.
1# توزیع فراوانی چیست؟
توزیع فراوانی (Frequency Distribution) یک نوع توزیع آماری است که احتمالا روش عملکرد آن از نامش قابل حدس زدن است.
در این روش توزیع آماری مشخص می شود که مقدار فراوانی هر داده چقدر است یا به طور ساده تر مشخص می کند که هر داده چند بار در گروه کلی داده ها موجود است.
این توزیع به منظور محاسبه شاخص های مرکزی (central Index) و شاخص پراکندگی (Dispersion Index) و مقایسه گروهی داده ها با گروه های دیگر جهت استنباط آماری تشکیل می شود.
همچنین لازم به ذکر است که به منظور طبقه بندی داده ها باید مرحله به مرحله دامنه تغییرات، تعداد طبقات، فاصله طبقات و انواع فراوانی ها با استفاده از فرمول هایی که در ادامه به بیان آن ها می پردازیم، محاسبه گردند.
در واقع می توان گفت که به نمایی کلی از همه مقادیر متمایز در برخی متغیرها و تعداد دفعات وقوع آن ها توزیع فراوانی می گویند.
لازم به ذکر است که فراوانی تعداد مشاهدات رخ داده در یک طبقه خاص است که با نماد f نمایش داده می شود.
ممکن است سوال پیش آید که بین فراوانی و توزیع فراوانی چه تفاوتی وجود دارد.
در واقع می توان گفت به تعداد مشاهدات در حال وقوع در یک طبقه خاص، فراوانی آن طبقه و یا فراوانی ساده می گوییم؛
ولی زمانی که ما فراوانی را در قالب یک جدول مرتب کنیم، به آن توزیع فراوانی می گوییم.
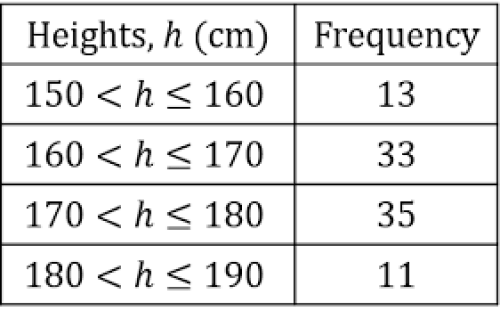
در مثال زیر توزیع فراوانی دانش آموزان یک پایه مدرسه براساس قد آن ها نوشته شده است.
برای نمایش جدول توزیع فراوانی عموما از نمودار های میله ای استفاده می شود؛ اما گاها نمودار دایره ای نیز در محاسبات مورد استفاده هستند.
در این جدول میزان فراوانی هر طبقه براساس یک ویژگی تقسیم بندی می شود.
این جدول به ما نشان می دهد که در یک مدرسه با 92 دانش آموز در یک پایه، 13 نفر از آن ها دارای قد بین 150 تا 160 سانتی متر هستند، 33 نفر بین 160 تا 170 سانتی متر، 35 نفر بین 170 تا 180 سانتی متر و در نهایت 11 نفر بین 180 تا 190 سانتی متر هستند.
نمودار میله ای مثال بالا به شکل زیر خواهد شد:
2# پارامترهای جدول توزیع فراوانی
هر جدول توزیع فراوانی می تواند یک یا چند مورد از پارامترهای زیر را با توجه به نیاز پروژه در بر بگیرد که
در ادامه به هر کدام از آن ها خواهیم پرداخت:
- دامنه تغییرات
- تعداد طبقات
- فاصله طبقات
- محاسبه انواع فراوانی
- محاسبه نقطه میانی هر طبقه
- محاسبه حدود واقعی طبقه
- میانگین داده ها

1-2# دامنه تغییرات داده ها
دامنه تغییرات را در جدول توزیع فراوانی می توان با استفاده از تفاضل بزرگ ترین عدد از کوچک ترین عدد به اضافه یک به دست آورد.
فرمول دامنه تغییرات به صورت زیر می باشد:
R=X2-X1+1
لازم به ذکر است که در صورت اعشاری بودن دامنه تغییرات عدد مورد نظر را باید گرد کرد.
در مثال عددی ذکر شده در ابتدای این مقاله دامنه تغییرات مساوی است با:
R = 190-150+1 = 41
2-2# تعداد طبقات جدول
محاسبه تعداد طبقات در اختیار محقق قرار دارد؛ اما معمولا برای جداول با دیتای زیاد تعداد آن ها بین 10 تا 20 طبقه می باشد.
دلیل این امر این می باشد که طبقات کمتر از 10 موجب بزرگ تر شدن اندازه طبقات و در نتیجه از دست رفتن اطلاعات می گردند.
همچنین طبقات بالاتر از 20 موجب طولانی شدن تهیه و تنظیم جدول می شود.
در جدول نمایش داده شده تعداد طبقات جدول به صورت تجربی 4 انتخاب شده است.
3-2# فاصله طبقات جدول توزیع فراوانی
لازم به ذکر است که فاصله همه طبقات در یک جدول توزیع فراوانی با هم برابر است.
همچنین اندازه فاصله طبقات یک عدد ثابت نمی باشد.
فاصله طبقات را می توان با استفاده از فرمول زیر به دست آورد:
تعداد طبقات (K) / دامنه تغییرات (R) = فاصله طبقات (I)
در مثال ذکر شده فاصله طبقات مطابق زیر به دست آمده است:
I = 41/4 = 10.25 ≈10
4-2# محاسبه انواع فراوانی
به منظور محاسبه توزیع فراوانی از انواع فراوانی ها در جدول استفاده می شود که عبارتند از:
- فراوانی مطلق: این نوع فراوانی با حرف f نشان داده می شود و از شمارش تعداد اعداد در یک طبقه به دست می آید.
لازم به ذکر است که مجموع فراوانی ها در تمام طبقات باید با مجموع اعداد (N) برابر باشد.
در مثال بیان شده این اعداد در ستون دوم جدول نوشته شده است که
در واقع مجموع تعداد دانش آموزان با قد مشخص شده در در هر محدوده طبقه است.
- فراوانی تراکمی: از جمع کردن فراوانی ها به صورت متوالی از پایین ترین طبقه تا بالاترین طبقه فراوانی تراکمی به دست می آید.
این فراوانی با cf نشان داده می شود. همچنین فراوانی تراکمی بالاترین طبقه با مجموع اعداد (N) برابر می باشد.
در مثال ذکر شده این اعداد از پایین به بالا در جدول برابرند با: 11، 46، 79 و 92
- فراوانی نسبی: فراوانی نسبی نشان دهنده میزان فضای اختصاص داده شده فراوانی یک طبقه نسبت به سایر طبقات می باشد که
می توان این نوع فراوانی را با Pf نشان داد.
فراوانی نسبی از فرمول زیر به دست می آید:
Pf = f/N
در مثال بیان شده فراوانی نسبی قد در بازه 170 تا 180 برابر است با:
pf = 35/92 = 0.38
- فراوانی نسبی درصدی: این فراوانی با p نمایش داده می شود و
نشان دهنده میزان فضای اشغال شده توسط فراوانی های یک طبقه بر اساس مقیاس 100 می باشد.
فرمول فراوانی نسبی درصدی به شرح زیر می باشد:
P=F/N*100
در مثال عددی قبل فراوانی نسبی درصدی مساوی است با: %38
5-2# محاسبه میانه در جدول توزیع فراوانی
در جدول توزیع فراوانی محاسبه میانه معمولا با xc نشان داده می شود و از طریق فرمول زیر به دست می آید:
2/(حد پایین طبقه + حد بالای طبقه) = xc
برای مثال ما میانه طبقه سوم برابر است با:
xc = (180 + 170) / 2 = 175
6-2# محاسبه حدود واقعی طبقه
در جدل توزیع فراوانی هر طبقه دارای یک حد واقعی می باشد که
نحوه محاسبه آن به صورت کم کردن نیم نمره از حد پایین طبقه و اضافه کردن نیم نمره به حد بالای طبقه به دست می آید.
7-2# محاسبه میانگین در جدول توزیع فراوانی
ابتدا باید فراوانی را در مرکز دسته ضرب کرد.
سپس تمام مقادیر به دست آمده در هر طبقه را جمع کرده و
در آخر تقسیم بر مجموع فراوانی ها کنیم و
به این صورت میانگین تقریبی همه داده ها به دست می آید.
برای مثال ذکر شده داریم:
15620 = 155*13 + 165*33 + 175*35 + 185*11
169.78 = 15620/92
 |
نظرتون درباره این مقاله چیه؟
ما رو راهنمایی کنید تا اون رو کامل تر کنیم و نواقصش رو رفع کنیم.
توی بخش دیدگاه ها منتظر پیشنهادهای فوق العاده شما هستیم.



ببخشید اگر فاصله طبقات در مد یکسان نبود در داده طبقه بندی چیکار کنیم؟
سلام همراه گرامی
از همراهی شما با سایت نماتک متشکریم.
با عرض پوزش ما یک مجموعه آموزشی هستیم و در زمینه های فنی ارائه خدمات و مشاوره و دانش مرتبط برای پاسخگویی به سوالات تخصصی عزیزان رو در بخش کامنت های سایت نداریم.
تنها راه پیشنهادی ما این هست که از فضای فروم نماتک برای دریافت راهنمایی استفاده بفرمایید تا عزیزانی که در این زمینه دانش و شناخت کافی دارند، پاسخگوی سوالات شما باشند.
آدرس فروم نماتک: https://katibeha.com/
موفق باشید.
جدول توزیع فراوانی برا چ پایه و رشته ای هست
سلام همراه گرامی
ما موسسه آموزشگاهی مهارتی هستیم و با عرض پوزش اطلاعاتی درباره کتب درسی مدارس نداریم
موید باشید
سلام بر شما ممنون خیلی روان و خوب بود توضیحاتتون فقط جسارتا جاهایی که نوشته شده مد منظورتون همان نقطه میانی هر طبقه هست؟
سلام دوست عزیز
سپاس از همراهی شما و محبت تون نسبت به مطالب نوشته شده
بله دقیقا منظور نقطه میانی بوده که برای رفع این ابهام برای سایر خوانندگان عبارات داخل متن مقاله تصحیح شدند.
از شما بابت بیان کردن این موضوع متشکریم.
موید و پیروز باشید
احسنت کاملا مبرهن و کامل و عام فهم ، سپاس فراوان، اجر حسنه نسیب تان باد
سلام همراه گرامی
از محبت شما ممنونیم و بسیار خوشحالیم که این مطلب برای شما مفید بوده
موفق باشید
لطفاً میشه شمارتو بذاربن تماس بگیرم
سلام خدمت شما دوست عزیز
خدمت شما:
02177926472
از همراهی شما با سایت نماتک سپاسگزار هستیم.
موفق باشید.
معلومات درباره جدول توزیع فراوانی خیلی عالی بود و در دانشگاه خیلی بدردم خورد
سلام خدمت شما بزرگوار
ممنون از اینکه نظر خودتان رو در سایت نماتک درج کردید.
از همراهی شما با سایت نماتک سپاسگزار هستیم.
موفق باشید.