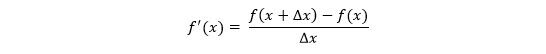روش تفاضل محدود یکی از روش های رایج در حل تقریبی معادلات دیفرانسیل جزئی است.
این روش حل در شرایط مختلفی قابل استفاده است و نتایج نسبتا دقیقی را در اختیار ما می گذارد.
در این مقاله قصد داریم به معرفی این روش بپردازیم.
تا انتها با ما همراه باشید.
1# روش تفاضل محدود چیست؟ (Finite Difference Method)
برای حل معادلات دیفرانسیل جزئی (Partial Differential Equations) نیاز به گسسته سازی آن ها داریم.
روش تفاضل محدود یک راه مستقیم برای گسسته سازی این معادلات است.
در این روش برای گسسته سازی معادلات به سراغ مکان می رویم.
به این معنی که به جای تحلیل یک معادله در یک مکان پیوسته، آن را به دو یا چند معادله در مکان های گسسته تبدیل می کنیم.
به این ترتیب تحلیل مسئله به مراتب آسان تر خواهد شد.
شبکه بندی در این روش به صورت مستطیلی و ساده انجام می شود.
به این معنی که در تحلیل مسئله از شبکه بندی منظم استفاده می کند.
2# تاریخچه روش تفاضل محدود
چندین نفر به عنوان پیشگامان حل معادلات دیفرانسیل جزئی با روش تفاضل محدود شناخته می شوند که عبارت اند از:
- لوییس فرای ریچاردسون (Lewis Fry Richardson)
- ریچارد ساوتول (Richard Southwell)
- ریچارد کورانت (Richard Courant)
- کرت فریدریکس (Kurt Friedrichs)
- هانس لوی (Hans Lewy)
- پیتر لاکس (Peter Lax)
- جان فون نویمان (John von Neumann)
در سال 1968 نخستین کاربرد عملی این روش در شبیه سازی انتشار امواج الاستیک ثبت شده است.

در سال 1992 این روش به حالت سه بعدی توسعه داده شد تا برای محاسبات پردازش موازی مورد استفاده قرار گیرد.
درحال حاضر نیز این روش برای بسیاری از تحلیل های عددی مورد استفاده قرار می گیرد.
3# روابط ریاضی تفاضل محدود
همان طور که اشاره کردیم، در این روش به سراغ گسسته سازی مسئله در بعد مکان می رویم.
به تصویر زیر نگاه کنید.
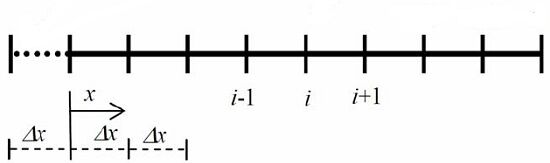
این تصویر نمودی از شبکه بندی یک بعدی برای تقریب تفاضل محدود مسئله است.
فواصل بین هر دو نقطه در این دسته بندی برابر Δx است.
البته باید توجه داشته باشید که لزومی بر مساوی بودن این فواصل بین گره های مختلف وجود ندارد.
با این وجود معمولا فواصل بین نقاط مختلف یکسان در نظر گرفته می شوند.
مشابه همین مفهوم برای شبکه بندی روش تفاضل محدود در دو یا سه بعد نیز استفاده می شود.
با ذکر این نکته باید اشاره کنیم که تقریب تفاضل محدود به سه روش قابل محاسبه است که عبارت اند از:
- تقریب تفاضل محدود پیشرو (Forward Difference Method)
در این روش برای گسسته سازی در کنار نقطه i به سراغ نقطه i+1 می رویم.
رابطه ریاضی روش تفاضل محدود پیشرو برای مشتق مرتبه اول به صورت زیر است:
تعمیم همین رابطه برای مشتق مرتبه دوم به صورت زیر است:
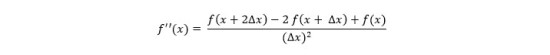
- تقریب تفاضل محدود مرکزی (Central Difference Method)
در این روش برای گسسته سازی دو نقطه قبل و بعد از نقطه i را استفاده می کنیم.
رابطه ریاضی روش تفاضل محدود مرکزی برای مشتق مرتبه اول به صورت زیر است:
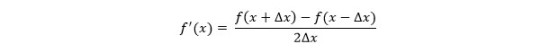
تعمیم همین رابطه برای مشتق مرتبه دوم به صورت زیر است:
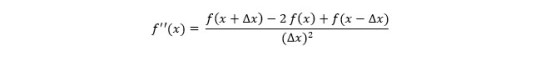
- تقریب تفاضل محدود پسرو (Backward Difference Method)
در این روش برای گسسته سازی در کنار نقطه i به سراغ نقطه i-1 می رویم.
رابطه ریاضی روش تفاضل محدود پسرو برای مشتق مرتبه اول به صورت زیر است:
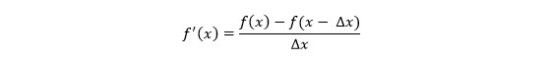
تعمیم همین رابطه برای مشتق مرتبه دوم به صورت زیر است:
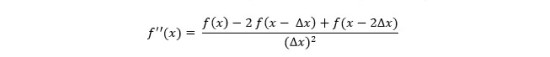
4# مزایا و معایب
در انتها قصد داریم نگاهی به مهم ترین مزایا و معایب استفاده روش تفاضل محدود بیندازیم.
به طور کلی دو مورد از مزایای اصلی این روش حل عددی عبارت اند از:
- امکان دستیابی به نتایج با دقت مرتبه بالاتر به کمک این روش وجود دارد.
- اجرای این روش در نرم افزار های حل عددی در مقایسه با روش حجم محدود و المان محدود به مراتب راحت تر است.
در کنار این موارد نباید از نقطه ضعف مهم این روش نیز غافل شد.
اگر به دنبال نتایج دقیق و تحلیل مسئله در شرایط مرزی آن هستیم، روش تفاضل محدود چندان کارآمد نیست.
به این دلیل که شبکه بندی منظم در حوالی مرز مسئله، دقت را به طور محسوسی کاهش می دهد.
جمع بندی
در این مقاله به بررسی روش تفاضل محدود در حل عددی معادلات دیفرانسیل خطی و جزئی پرداختیم.
این روش برای حل بسیاری از معادلات دیفرانسیل پیچیده در حوزه های مختلف از جمله هواشناسی، اختر فیزیک و لرزه نگاری مورد استفاده قرار می گیرد.
در بسیاری از نرم افزار های کاربردی مانند فلوئت (Fluent)، کامسول (Comsol) و… نیز از این روش برای حل عددی معادلات دیفرانسیل استفاده می شود.
در نهایت یادگیری این روش به عنوان یکی از بهترین ابزارهای حل عددی معادلات دیفرانسیل برای متخصصان و مهندسان از اهمیت بالایی برخوردار است.
 |
نظرتون درباره این مقاله چیه؟
ما رو راهنمایی کنید تا اون رو کامل تر کنیم و نواقصش رو رفع کنیم.
توی بخش دیدگاه ها منتظر پیشنهادهای فوق العاده شما هستیم.