کمانش یک مفهوم مکانیکی مهم است که به خصوص در طراحی و ساخت تیرها و ستون ها باید مد نظر قرار بگیرد.
بعضا شاهد هستیم که بی توجهی به تحمل تیرها و ستون ها در برابر بارهای فشاری محوری، خسارت های جدی را در سازه ها به بار می آورد.
بنابراین شما باید در طراحی و ساخت محصولات آن ها را در نظر بگیرید.
در این مطلب قصد داریم به بررسی مفهوم کمانش و نحوه محاسبه حداکثر تنش فشاری محوری قابل تحمل توسط یک ستون بپردازیم.
حتما تا پایان این مطلب با ما همراه باشید.
1# کمانش چیست؟ (Buckling)
به زبان ساده کمانش به پدیده ای اشاره می کند که به کمک آن رفتار یک سازه تحت نیروهای فشاری محوری توصیف می شود.
اجازه دهید یک مثال بزنیم.
یک نی را بردارید و بین دو انگشت اشاره خود نگه دارید.
سپس به آرامی با دو انگشت خود به نی فشار بیاورید و مقدار فشار وارد شده را کم کم افزایش دهید.
در ابتدا که مقدار فشار کم است، تغییری در حالت نی به وجود نمی آید؛ اما بعد از مدتی با افزایش نیروی فشاری، نی شروع به خم شدن می کند.
دقیقا مشابه همین اتفاق نیز ممکن است برای تیرها و ستون ها رخ دهد.
با استفاده از مفهوم کمانش میزان مقاومت یک تیر یا ستون در برابر بارهای فشاری محوری، سنجیده می شود.
بعد از خم شدن سازه در اثر کمانش، احتمال وقوع اتفاقاتی مانند تاب برداشتن یا شکستن آن وجود دارد.

با توجه به توضیحاتی که تا اینجا اشاره کردیم، لازم است روی یک نکته مهم تمرکز کنیم.
مفهوم Buckling تنها با نیروهای فشاری وارد به سازه ها معنی پیدا می کند.
آن هم نیروی فشاری که به سطح مقطع کوچک تر سازه وارد می شود.
یک میله استوانه ای را در نظر بگیرید.
خم شدن میله در اثر نیروهایی که عمود بر محور مرکزی آن وارد می شوند را نباید با کمانش اشتباه بگیرید.
پدیده Buckling تنها در اثر نیروهای هم راستا با محور سطح مقطع میله رخ می دهد.
2# انواع کمانش
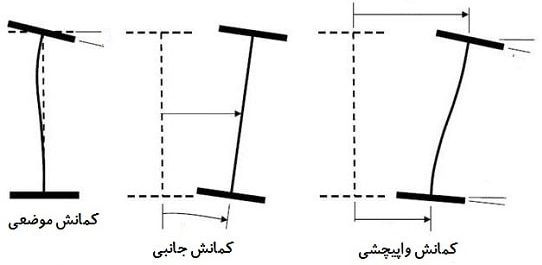
پدیده کمانش در تیرها و ستون ها به سه شکل مختلف رخ می دهد که عبارت اند از:
- جانبی
- موضعی
- واپیچشی
در حالت جانبی، تیر یا ستون خم نمی شود؛ بلکه سطح مقطع آن حول محور شروع به چرخیدن می کند.
به عبارت دیگر نوعی جابهجایی مکانی سطح مقطع تیر را نسبت به موقعیت اولیه خود شاهد هستیم.
این در حالی است که کمانش موضعی به طور مشخص در اثر خم شدن تیر ناشی از نیروی فشاری رخ می دهد.
علاوه بر آن امکان دارد که با وارد شدن نیروی فشاری همزمان شاهد خم شدن تیر و جابهجایی سطح مقطع آن باشیم.
اگر این دو اتفاق به صورت همزمان با هم رخ دهند، اصطلاحا تحت عنوان کمانش واپیچشی از آن یاد می شود.
3# عوامل موثر در کمانش تیرها و ستون ها
چند عامل کلیدی را بر میزان مقاومت سازه ها در برابر نیروهای فشاری محوری موثر هستند که عبارت اند از:
- طول سازه
- شکل و مساحت سطح مقطع سازه
- خاصیت کشسانی سازه
- نوع تکیه گاه های سازه
هر چه طول سازه بیشتر و سطح مقطع آن باریک تر باشد، مقاومت آن در برابر نیروهای فشاری محوری کاهش پیدا می کند.
به همین دلیل احتمال کمانش آن با نیروی فشاری کم نیز وجود دارد.
دلیل اینکه معمولا سطح مقطع دو سر تیرها و ستون ها نسبت به وسط آن ها بزرگ تر طراحی می شود نیز افزایش مقاومت آن ها در برابر نیروهای فشاری است.

خاصیت کشسانی و صلبیت سازه ها در نوع واکنش آن ها در اثر کمانش تاثیرگذار هستند.
هر چه صلبیت قطعه بیشتر و خاصیت کشسانی آن کمتر باشد، در اثر کمانش زودتر می شکند.
به عنوان مثال یک رشته ماکارونی را با نی که بالاتر اشاره کردیم، مقایسه کنید.
در اثر نیرو و فشار، نی به راحتی نمی شکند؛ اما رشته ماکارونی اصلا حالت کشسانی ندارد و فورا می شکند.
اساسا برای انتخاب تیر یا ستون مناسب نباید تنها بارگذاریهای عرض را مد نظر قرار دهید.
گاهی اوقات این امکان وجود دارد که میزان بار بحرانی محوری تیز نسبت به تنش تسلیم ناشی از بارهای عرضی به مراتب کمتر باشد.
در چنین شرایطی طبیعی است که در اثر بارهای محوری سازه خیلی زودتر آسیب می بیند.
به همین دلیل گاهی اوقات باید مبنای انتخاب تیر یا ستون ساختمان را بر اساس میزان بار بحرانی طولی در نظر بگیرید.
4# محاسبه میزان Buckling تیرها و ستون ها
محاسبه میزان کمانش تیرها و ستون ها بر اساس نیروی فشاری محوری که به آن ها وارد می شود، امکان پذیر است.
برای این منظور باید یک معادله دیفرانسیل ریاضی را حل کنید.
در این جا با ذکر یک مثال نحوه محاسبه کمانش تیر یک سر درگیر را که مطابق تصویر زیر تحت نیروی فشاری P قرار دارد، بررسی می کنیم.
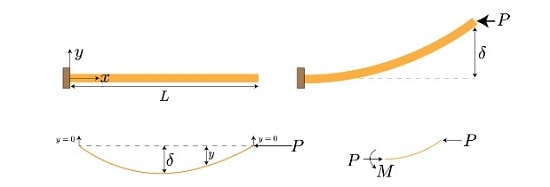
همان طور که مشاهده می کنید، در اثر وارد شدن نیروی P، تیر به سمت بالا کمانش پیدا می کند.
مقدار انحراف تیر براساس یک معادله دیفرانسیل خطی درجه دوم محاسبه می شود که به صورت زیر است.
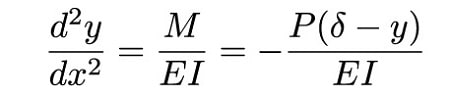
- y: محور مختصات در راستای عمود بر تیر
- X: محور مختصات در راستای محور تیر
- M: گشتاور واردشده به محل تکیه گاه تیر
- E: مدول الاستیسیته تیر
- I: ممان اینرسی سطح مقطع تیر
- ∂: میزان انحراف تیر در اثر کمانش در هر نقطه
برای ساده سازی رابطه ریاضی فوق از یک فاکتور استفاده می شود که به صورت زیر است.
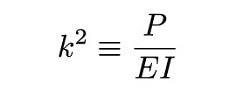
بر این اساس رابطه ریاضی مربوط به محاسبه میزان انحراف تیر در اثر کمانش به صورت زیر در می آید.
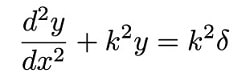
با استفاده شرایط مرزی می توان معادله دیفرانسیل فوق را حل کرد.
هدف اصلی از حل معادله دیفرانسیل فوق، به دست آوردن بار بحرانی است که در اثر کمانش منجر به شکست تیر می شود.
بر این اساس میزان نیروی بحرانی که منجر به شکست تیر می شود به صورت زیر حاصل می شود.
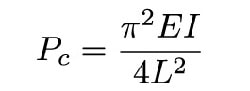
دقت داشته باشید که این رابطه فقط برای تیر یک سر درگیر است که در محل تکیه گاه آن از پین استفاده می شود.
برای سایر تیرها و ستون ها با شرایط بارگذاری و تکیه گاه مختلف، باید محاسبات جداگانه به منظور محاسبه بار بحرانی انجام داد.
 |
نظرتون درباره این مقاله چیه؟
ما رو راهنمایی کنید تا اون رو کامل تر کنیم و نواقصش رو رفع کنیم.
توی بخش دیدگاه ها منتظر پیشنهادهای فوق العاده شما هستیم.


