ماتریس سردرگمی چیست و چه معیارهایی دارد؟

راه‌های زیادی برای ارزیابی مدل طبقه‌بندی شما وجود دارد؛ اما ماتریس سردرگمی یکی از قابل‌ اعتمادترین گزینه‌ها است.

این نشان می‌دهد که مدل شما چقدر خوب عمل کرده و کجا خطا داشته است و به شما کمک می‌کند تا پیشرفت کنید.

مبتدیان اغلب ماتریس سردرگمی را گیج کننده می‌دانند؛ اما در واقع ساده و قدرتمند است.

در این مقاله، ما به جزئیات ماتریس سردرگمی، اهمیت آن در یادگیری ماشین و چگونگی استفاده از آن برای بهبود عملکرد مدل‌های طبقه‌بندی خواهیم پرداخت.

1# ماتریس سردرگمی چیست؟

متخصصان یادگیری ماشین و دانشمندان داده متوجه شده‌اند که الگوریتم‌های هوش مصنوعی کامل نیستند و مستعد خطا هستند.

اصولاً این متخصصان باید بفهمند که الگوریتم چه خطاهایی مرتکب می‌شود.

این فرایند آنها را قادر می‌سازد تا الگوریتم را بهبود بخشند و مدلی بسازند که ارزش کسب‌وکار را افزایش دهد و درعین‌حال احتمال خطا را کاهش دهد.

این فرایند که «متریک‌های ارزیابی» نامیده می‌شود، شامل انواع مختلفی (مانند ناحیه زیر منحنی) است، همچنین به عنوان AUC  شناخته می‌شود.

حتی برخی از سازمان‌ها معیارهایی را طراحی می‌کنند که با شاخص‌های کلیدی عملکرد (به‌اختصار KPI) یا مشکلات تجاری منحصربه‌فردشان هماهنگی بهتری داشته باشد.

یکی از این اندازه‌گیری‌های رایج عملکرد برای وظایف طبقه‌بندی، ماتریس سردرگمی نامیده می‌شود.

ماتریس‌های سردرگمی یا در اصطلاحی دیگر ماتریس درهم ریختگی ابزارهای اندازه‌گیری عملکرد هستند که معمولاً برای وظایف طبقه‌بندی یادگیری ماشین استفاده می‌شوند و به‌ویژه برای اندازه‌گیری صحت و دقت، یادآوری و ویژگی یک مدل طبقه‌بندی مفید هستند.

ماتریس‌های سردرگمی زمانی به کار می‌روند که خروجی مدل می‌تواند دو یا چند کلاس باشد. (یعنی طبقه‌بندی چند کلاسه و طبقه‌بندی باینری)

یا ماتریس سردرگمی در یادگیری ماشین، ماتریسی از اعداد است که به دانشمند داده نشان می‌دهد که مدل آنها در کجا اشتباه می‌شود.

این یک توزیع کلاسی از عملکرد پیش‌بینی مدل طبقه‌بندی است، یک روش سازمان‌یافته برای نگاشت پیش ‌بینی‌ها به کلاس‌های اصلی که داده‌ها به آن تعلق دارند.

ماتریس تعداد پیش‌بینی‌های صحیح و نادرست را با مقادیر شمارش خلاصه می‌کند و آنها را بر اساس هر کلاس تقسیم می‌کند.

به‌ این‌ ترتیب، دانشمند داده در مورد خطاهایی که طبقه‌بندی‌کننده مرتکب می‌شود و مهم‌تر از آن، انواع خطاهایی که انجام می‌دهد، بینشی به دست می‌آورد.

2# چرا به ماتریس‌های سردرگمی نیاز داریم؟

ماتریس‌های سردرگمی ضروری هستند؛ زیرا درک بهتری از نحوه عملکرد یک مدل نسبت به‌دقت طبقه‌بندی به ما می‌دهند.

با استفاده از آن بهتر می‌توانید درک کنید که مدل طبقه‌بندی تا چه حدی درست است؛ زیرا ماتریس مستقیماً مقادیری مانند مثبت واقعی، مثبت کاذب، منفی واقعی و منفی کاذب را مقایسه می‌کند.

از دلایل نیاز به ماتریس درهم ریختگی می‌توان به موارد زیر اشاره کرد:

• آنها جزئیات خطاهای طبقه‌بندی‌کننده و همچنین انواع خطاهایی را که در حال رخ دادن هستند، توضیح می‌دهند.
• آنها نشان می‌دهند که چگونه پیش‌بینی‌ها توسط یک مدل طبقه‌بندی انجام می‌شود که نیاز به شفاف‌سازی و سازماندهی بیشتری دارد.
• آنها به غلبه دقت طبقه‌بندی بر ایرادات وابسته کمک می‌کنند.
• آنها را می‌توان در شرایطی استفاده کرد که یک طبقه بر سایرین تسلط دارد و کل مشکل طبقه‌بندی باید متعادل‌تر باشد.
• آنها می‌توانند به طور مؤثر و موفقیت‌آمیزی صحت، دقت، یادآوری، ویژگی و منحنی AUC-ROC را محاسبه کنند.

به‌ خاطر داشته باشید که اگر تعداد مشاهدات نابرابر در هر کلاس وجود داشته باشد یا اگر مجموعه‌داده شما بیش از دو کلاس داشته باشد، دقت طبقه‌بندی به‌خودی‌خود می‌تواند گمراه‌کننده باشد.

ماتریس‌های سردرگمی به این موضوع می‌پردازند و به شما ایده واضح‌تری از اینکه مدل درست انجام می‌دهد، کجا کوتاه می‌آید و چه نوع خطاهایی انجام می‌دهد، به شما خواهند داد.

3# ساختار ماتریس سردرگمی

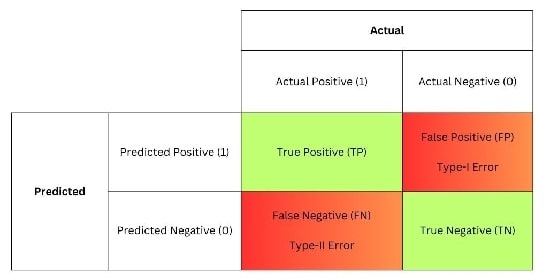
ماتریس سردرگمی یک ابزار ارزیابی عملکرد است که عملکرد یک مدل طبقه‌بندی را با جدول‌بندی پیش‌بینی‌های مثبت درست، منفی درست، مثبت کاذب و منفی کاذب خلاصه می‌کند.

به‌طورکلی، ماتریس درهم ریختگی یک نمای دانه‌ای از عملکرد یک مدل در کلاس‌های مختلف ارائه می‌دهد.

این ماتریس بر اساس مفاهیم مثبت واقعی (TP)، منفی واقعی (TN)، مثبت کاذب (FP) و منفی کاذب (FN) است که توضیح این مفاهیم به‌ صورت زیر است:

1-3# مثبت واقعی (TP)

مواردی که در آن، مدل یک کلاس مثبت را به‌درستی پیش‌بینی می‌کند در حالی‌ که واقعاً مثبت است.

یک مدل تشخیصی سرطان را در نظر بگیرید: زمانی که مدل به‌ درستی بیمار مبتلا به سرطان را به عنوان مبتلا به این بیماری شناسایی کند، یک مثبت واقعی رخ می‌دهد.

TP یک معیار حیاتی برای توانایی مدل در تشخیص دقیق موارد مثبت است.

2-3# منفی‌های واقعی (TN)

مواردی که مدل به‌درستی یک کلاس منفی را زمانی که واقعاً منفی است پیش‌بینی می‌کند.

در ادامه تشبیه پزشکی، یک منفی واقعی زمانی خواهد بود که مدل به‌درستی یک بیمار سالم را فاقد بیماری شناسایی کند.

TN نشان‌دهنده مهارت مدل در تشخیص موارد منفی است.

3-3# موارد مثبت کاذب (FP)

مواردی که در آن، مدل یک کلاس مثبت را به اشتباه پیش‌بینی می‌کند در حالی‌ که باید منفی می‌بود.

در سناریوی پزشکی، مثبت کاذب به این معنی است که مدل به اشتباه نشان می‌دهد که یک بیمار به این بیماری مبتلا است درحالی‌که در واقع سالم است.

FP مواردی را نشان می‌دهد که در آن مدل اعتماد بیش از حد را در پیش‌بینی نتایج مثبت نشان می‌دهد.

4-3# منفی‌های کاذب (FN)

مواردی که در آن مدل یک کلاس منفی را به اشتباه پیش‌بینی می‌کند درحالی‌که باید مثبت می‌بود.

در زمینه پزشکی، منفی کاذب زمانی است که مدل نتواند بیماری را در بیمار که واقعاً به آن مبتلا است، تشخیص دهد.

FN موقعیت‌هایی را برجسته می‌کند که در آن مدل نتواند نمونه‌های مثبت واقعی را ثبت کند.

4# محاسبه ماتریس سردرگمی

در این بخش نحوه محاسبه ماتریس سردرگمی تنها در چند مرحله ساده آورده شده است:

• یک مجموعه‌داده اعتبارسنجی یا مجموعه‌داده آزمایشی با مقادیر نتیجه مورد انتظار به دست آورید.
• برای هر ردیف در مجموعه‌داده‌های آزمایشی پیش‌بینی کنید.
• از نتایج و پیش‌بینی‌های مورد انتظار خود، موارد زیر را بشمارید:
  • تعداد پیش‌بینی‌های صحیح هر کلاس
  • تعداد پیش‌بینی‌های نادرست هر کلاس که توسط کلاس پیش‌بینی‌شده مرتب می‌شود.
• این اعداد را در یک جدول یا یک ماتریس مانند مدل زیر سازماندهی کنید:
  • هر ردیف ماتریس مربوط به یک کلاس پیش‌بینی‌شده است. (انتظار می‌رود در سمت پایین)
  • هر ستون ماتریس مربوط به یک کلاس واقعی است. (پیش‌بینی‌ شده در بالای صفحه)
• تعداد طبقه‌بندی صحیح و نادرست را در جدول پر کنید.
• تعداد کل پیش‌بینی‌های صحیح برای یک کلاس به ردیف مورد انتظار برای آن مقدار کلاس و ستون پیش‌بینی‌شده برای آن مقدار کلاس وارد می‌شود.
• تعداد کل پیش‌بینی‌های نادرست برای یک کلاس وارد ردیف مورد انتظار برای آن مقدار کلاس و ستون پیش‌بینی‌شده برای آن مقدار کلاس می‌شود.

5# معیارهای ارزیابی بر اساس داده‌های ماتریس سردرگمی

باتوجه‌به این که ماتریس سردرگمی ابزار ارزشمندی برای ارزیابی اثربخشی مدل‌های طبقه‌بندی است.

چندین معیار عملکرد را می‌توان از داده‌های درون ماتریس سردرگمی به دست آورد.

برخی از پرکاربردترین آنها را به شرح زیر هستند:

1-5# صحت

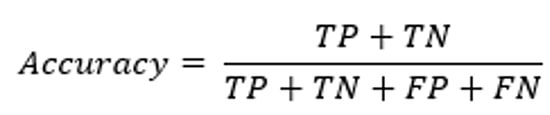
صحت یک معیار اساسی است که درستی کلی پیش‌بینی‌های مدل را اندازه‌گیری می‌کند.

این به عنوان مجموع مثبت و منفی واقعی تقسیم بر تعداد کل نمونه‌ها محاسبه می‌شود.

2-5# دقت

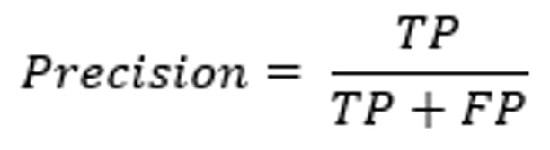
دقت،توانایی مدل را برای شناسایی صحیح موارد مثبت از مجموع موارد مثبت پیش‌بینی‌شده، برازش می‌کند.

دقت بر پیش‌بینی‌های مثبت تمرکز دارد. این معیار به عنوان نسبت مثبت واقعی به مجموع مثبت واقعی و مثبت کاذب محاسبه می‌شود.

3-5# یادآوری / حساسیت

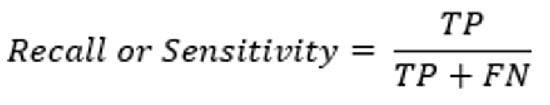
یادآوری که به عنوان حساسیت یا نرخ مثبت واقعی نیز شناخته می‌شود، توانایی مدل را در طبقه‌بندی صحیح موارد مثبت از مجموع موارد مثبت واقعی اندازه‌گیری می‌کند.

این به عنوان نسبت مثبت واقعی به مجموع مثبت واقعی و منفی کاذب محاسبه می‌شود.

4-5# ویژگی یا نرخ منفی واقعی

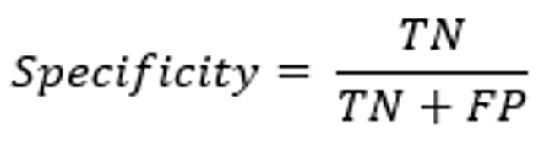
ویژگی، یا نرخ منفی واقعی، توانایی مدل را برای شناسایی صحیح موارد منفی از میان همه موارد منفی واقعی می‌سنجد.

این قابلیت مدل را برای شناسایی صحیح موارد منفی ارزیابی می‌کند. ویژگی به عنوان نسبت منفی واقعی به مجموع منفی واقعی و مثبت کاذب محاسبه می‌شود.

5-5# نرخ اشتباه یا نرخ منفی کاذب

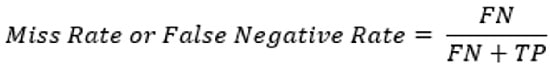
نرخ اشتباه، همچنین به عنوان نرخ منفی کاذب شناخته می‌شود، نشان‌دهنده نسبت مثبت‌های واقعی است که به اشتباه به عنوان منفی طبقه‌بندی شده‌اند.

Miss Rate تمایل مدل به از دست دادن موارد مثبت را ارزیابی می‌کند.

این به عنوان نسبت منفی‌های کاذب به مجموع منفی‌های کاذب و مثبت واقعی محاسبه می‌شود.

6-5# نرخ سقوط یا مثبت کاذب

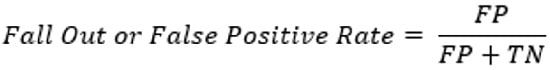
نرخ افت یا مثبت کاذب، نسبت منفی‌های واقعی را که به اشتباه به عنوان مثبت طبقه‌بندی شده‌اند، برازش می‌کند.

این به عنوان نسبت مثبت‌های کاذب به مجموع مثبت‌های کاذب و منفی‌های واقعی محاسبه می‌شود.

7-5# امتیاز F1

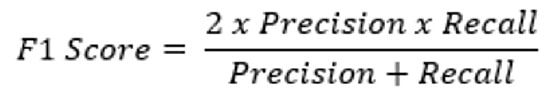
امتیاز F1 یک میانگین هارمونیک از دقت و یادآوری است.

این امتیاز در ماتریس سردرگمی، هر دو معیار را در یک ارزش واحد ترکیب می‌کند که نشان‌دهنده عملکرد خوب مدل در هر دو کلاس مثبت و منفی است.

از نظر ریاضی می‌توانیم آن را به‌صورت زیر بنویسیم:

در یادگیری ماشینی، مدل ایده‌آل به طور کامل همه موارد مربوطه (یادآوری بالا) را بدون هیچ اشتباهی (دقت بالا) شناسایی می‌کند.

با این‌ حال، این اغلب غیرواقعی است، در عمل، زمانی که ما سعی می‌کنیم دقت مدل خود را افزایش دهیم، متعاقباً فراخوان کاهش می‌یابد و بالعکس.

از این ‌رو، امتیاز F1 به ما کمک می‌کند تا با ترکیب هر دو معیار در یک مقدار واحد، این معامله را انجام دهیم.

این معیار از 0 تا 1 متغیر است که در آن 0 به معنای عملکرد ضعیف و 1 به معنای عملکرد عالی است.

امتیاز F1 زمانی مفید است که بخواهیم مدل‌های مختلف را با هم مقایسه کنیم یا هایپرپارامترها را تنظیم کنیم.

6# بهبود مدل در ماتریس سردرگمی

برای بهبود مدل در ماتریس سردرگمی چند راهکار ارائه می‌شود.

از جمله این راهکارها می‌توان به موارد زیر اشاره کرد:

1-6# بهبود موارد مثبت واقعی و منفی واقعی

بهبود TP و TN به معنای افزایش دقت کلی مدل است که نسبت تعداد پیش‌بینی‌های صحیح از همه پیش‌بینی‌ها است.

در اینجا چند تکنیک برای انجام این کار وجود دارد:

از استفاده از مجموعه‌داده‌های برچسب‌گذاری شده با کیفیت بالا و دقیق اطمینان حاصل کنید.

تمیز کردن و تقویت داده‌ها و عدم تعادل کلاس آدرس را در صورت لزوم در نظر بگیرید.

آزمایش را با الگوریتم‌ها یا معماری‌های مختلف، مانند الگوریتم‌های سری YOLO که ممکن است با پیچیدگی مشکل و ویژگی‌های داده، بیشتر همسو باشد، انجام دهید.

فراپارامترهای الگوریتم انتخابی را با استفاده از جستجوی شبکه‌ای، جستجوی تصادفی و یا بهینه‌سازی Bayesian، برای معیار خاصی (به‌ عنوان‌ مثال، امتیاز F1 و AUC ROC) که می‌خواهید بهبود دهید، بهینه کنید، از تکنیک‌هایی مانند کیسه‌بندی، تقویت و چیدمان برای ترکیب مدل‌ها برای تعمیم‌پذیری و استحکام بهتر استفاده کنید.

2-6# کاهش مثبت کاذب و منفی کاذب

کاهش FP و FN به معنای کاهش میزان خطای کلی مدل است که نسبت پیش‌بینی‌های نادرست از همه پیش‌بینی‌ها است. نحوه انجام این کار به‌صورت زیر است:

برای هر کلاس از رویکردهای مناسب استفاده کنید (مثلاً نمونه‌برداری یا نمونه‌سازی بیش از حد از کلاس اقلیت و تنظیم وزن طبقات با استفاده از آستانه‌های کلاسی خاص).

یک ماتریس هزینه را در تابع ضرر در طول تمرین بگنجانید تا انواع خاص خطاها را به شدت جریمه کنید.

ویژگی‌های جدید یا آموزنده‌ترین‌ها را انتخاب کنید تا توانایی مدل در تمایز بین کلاس‌ها را افزایش دهید.

برای کاهش پیچیدگی مدل و جلوگیری از تطبیق بیش از حد که منجر به نرخ بالای FP یا FN می‌شود، از تکنیک‌هایی مانند منظم کردن یا ترک تحصیل L1 یا L2 استفاده کنید.

موارد آموزنده را از کاربر یا متخصص جویا شوید تا به طور فعال عملکرد مدل را در مناطقی که در آن مشکل دارد، بهبود بخشد.

داده‌های بدون برچسب را در ارتباط با داده‌های برچسب‌گذاری شده برای کمک به مدل در یادگیری مؤثرتر به‌ویژه زمانی که داده‌های برچسب‌گذاری شده کمیاب هستند، استفاده کنید.

7# کاربردهای ماتریس سردرگمی

ماتریس سردرگمی در زمینه‌های مختلف کاربرد دارد:

• ارزیابی مدل: کاربرد اولیه ماتریس سردرگمی ارزیابی عملکرد یک مدل طبقه‌بندی است که بینش‌هایی در مورد صحت، دقت، فراخوانی و امتیاز F1 مدل ارائه می‌دهد.
• تشخیص پزشکی: ماتریس سردرگمی کاربرد گسترده‌ای در زمینه‌های پزشکی برای تشخیص بیماری‌ها بر اساس آزمایش‌ها یا تصاویر پیدا می‌کند.
  این به افزایش دادن دقت تست‌های تشخیصی و شناسایی تعادل بین مثبت کاذب و منفی کاذب کمک می‌کند.
• تشخیص تقلب: بانک‌ها و مؤسسات مالی از ماتریس‌های درهم ریختگی برای شناسایی تراکنش‌های جعلی استفاده می‌کنند و نشان می‌دهند که چگونه الگوریتم‌های هوش مصنوعی به شناسایی الگوهای فعالیت‌های متقلبانه کمک می‌کنند.
• پردازش زبان طبیعی (NLP): مدل‌های NLP از ماتریس‌های سردرگمی برای ارزیابی تحلیل احساسات، طبقه‌بندی متن و شناسایی موجودیت نام‌گذاری شده استفاده می‌کنند.
• پیش‌بینی ریزش مشتری: ماتریس‌های سردرگمی نقشی اساسی در پیش‌بینی ریزش مشتری دارند و نشان می‌دهند که چگونه مدل‌های مبتنی بر هوش مصنوعی از داده‌های تاریخی برای پیش‌بینی و کاهش ریزش مشتری استفاده می‌کنند.
• تشخیص تصویر و اشیا: ماتریس‌های درهم ریختگی به مدل‌های آموزشی برای شناسایی اشیا در تصاویر کمک می‌کنند و فناوری‌هایی مانند ماشین‌های خودران و سیستم‌های تشخیص چهره را قادر می‌سازند.
• تستA/B: تست A/B برای بهینه سازی تجربیات کاربر بسیار مهم است.
  ماتریس‌های سردرگمی به تجزیه و تحلیل نتایج آزمون‌های A/B کمک می‌کنند و تصمیمات مبتنی بر داده را در استراتژی‌های تعامل کاربر ممکن می‌سازند.

8# مزایای ماتریس سردرگمی

ماتریس سردرگمی با ارائه راهکارهای مفید در طبقه‌بندی مزایای زیادی را در دسترس قرار می‌دهد، من الجمله:

• حل داده‌های نامتعادل: استفاده از صحت به عنوان یک معیار مستقل محدودیت‌هایی برای داده‌های نامتعادل دارد و استفاده از معیارهای دیگر، مانند دقت و یادآوری، امکان دید متعادل‌تر و نمایش دقیق‌تر را فراهم می‌کند.
  به عنوان مثال، مثبت کاذب و منفی کاذب می‌تواند منجر به پیامدهای زیادی در بخش‌هایی مانند امور مالی شود.
• متمایزکننده نوع خطا: درک انواع مختلف خطاهای تولید شده توسط مدل یادگیری ماشین، دانشی در مورد محدودیت‌ها و زمینه‌های بهبود آن فراهم می‌کند.
• معاوضه‌ها: معاوضه بین استفاده از معیارهای مختلف در یک ماتریس درهم ریختگی ضروری است؛ زیرا آنها بر یکدیگر تأثیر می‌گذارند.
  به عنوان مثال، افزایش دقت به طور معمول منجر به کاهش در یادآوری می‌شود.
  این شما را در بهبود عملکرد مدل با استفاده از دانش حاصل از مقادیر متریک تاثیرگذار راهنمایی می‌کند.

9# اهمیت ماتریس سردرگمی در یادگیری ماشین

مدل‌های یادگیری ماشین به طور فزاینده‌ای در برنامه‌های مختلف برای طبقه‌بندی داده‌ها به دسته‌های مختلف استفاده می‌شوند.

با این‌ حال، ارزیابی عملکرد این مدل‌ها برای اطمینان از دقت و قابلیت اطمینان آنها بسیار مهم است یکی از ابزارهای ضروری در این فرایند ارزیابی، ماتریس سردرگمی است.

این یک معیار عملکرد برای مشکلات طبقه‌بندی یادگیری ماشین با دو یا چند کلاس به عنوان خروجی است.

دقت کلی مدل هنگام استفاده از مجموعه‌داده‌های قطار و آزمایش مشابه و بالا است.

حتی معیارها در سطح کلاس مشابه و بالا هستند. در استفاده از این ماتریس، ممکن است به این نتیجه برسیم که مدل SVC به‌درستی کالیبره شده است و قادر به پیش‌بینی دقیق در مجموعه ‌داده‌های آزمون از نظر دقت عمومی و سطح کلاس است.

اساساً، یک ماتریس سردرگمی می‌تواند به مدل‌های طبقه‌بندی یادگیری ماشین کمک کند تا بهتر و سریع‌تر عمل کنند.

نتیجه گیری

ماتریس سردرگمی ابزار ارزشمندی برای ارزیابی چگونگی عملکرد یک مدل طبقه‌بندی است.

این ماتریس با تجزیه و تحلیل پیش‌بینی‌های صحیح و نادرست (مثبت‌های واقعی، منفی‌های واقعی، مثبت‌های کاذب و منفی‌های کاذب) بینش‌های روشنی در مورد معیارهای مهم مانند صحت، دقت، و یادآوری ارائه می‌دهد.

یکی از موارد مهم مورد استفاده از ماتریس درهم ریختگی علم پزشکی و تشخیص بیماری‌ها است.

با درک و استفاده از معیارهای ماتریس سردرگمی، پزشکان می‌توانند تصمیمات بهتری را به خصوص زمانی که با مجموعه‌داده‌های نامتعادل سروکار دارند، در مورد عملکرد مدل اتخاذ کنند.