اعداد باینری یکی از انواع روش های نمایش اعداد هستند که مورد استفاده سیستم های دیجیتالی یا زبان های برنامه نویسی قرار می گیرند.
اگر قصد دارید به دنیای دیجیتال یا برنامه نویسی وارد شوید، ابتدا باید به خوبی با مفهوم عدد باینری و روش های پیاده سازی اعمال ریاضیاتی بر روی آن آشنا باشید.
در ادامه این مقاله و ویدیوی موجود به بیان بسیار ساده شما را با اعداد باینری که به آن ها اعداد دودویی نیز گفته می شود، آشنا می کنیم.
1# اعداد باینری چیست؟
در واقع عددهای باینری، اعدادی هستند که در دنیای ریاضیات و الکترونیک دیجیتال در مبنای 2 بیان می شوند.
وقتی یک مبنای N برای اعداد تعریف میکنیم، به این معنی است که بازه های عددی در آن از 0 تا N-1 را شامل می شوند.
برای مثال مبنای ده (یا همین اعداد دهدهی که روزمره به کار میبریم) شامل ارقام 0 تا 9 است.
به بازه اعداد باینری، عدد دودویی نیز گفته می شود.
برای نمایش اعداد در مبنای دودویی همانطور که در مثال بالا گفته شد از یک رشته عدد 0 و 1 استفاده می شود.
در فیلم بالا با مفهوم 0 و 1 ها و اینکه این 0 و 1 ها در واقع معادل سطح ولتاژهای پایین و بالا هستند، آشنا شدیم.
انواع اعداد باینری را دیدیم و حالا می خواهیم که به طور کاملتر به تبدیل مبناها بپردازیم.
2# مفهوم بیت و بایت (bit & Byte)
به هر رقم در یک عدد باینری بیت (bit) گفته می شود.
برای مثال یک رشته عدد 001010، دارای 6 رقم یا 6 بیت است.
از آنجایی که در دنیای دیجیتال و کامپیوتر به صورت معمول هر رشته عدد شامل 8 بیت است، برای این دسته ها نامگذاری جداگانه ای صورت گرفته است.
به هر 8 بیت پشت سر هم یک بایت (Byte) گفته می شود.
نکته: توجه داشته باشید که برای استفاده از حروف اختصاری، بیت را با حرف “b” کوچک و هر بایت را با “B” بزرگ نمایش میدهند.
3# تبدیل مبنای 10 به 2
در اولین گام، بررسی می کنیم که چگونه یک عدد در مبنا 10 (دسیمال) را به یک مبنای دلخواه ببریم:
- در اولین مرحله، عدد مورد نظر مان را به 2 تقسیم می کنیم.
- سپس در هر مرحله بعدی، خارج قسمت را بر 2 تقسیم می کنیم
این روند به قدری ادامه پیدا می کند که خارج قسمت از 2 کمتر شود. - سپس آخرین خارج قسمت و باقی مانده های هر مرحله (از آخر به اول) را به ترتیب در کنار هم می نویسم.
- عدد بدست آمده، عدد مورد نظر ما در مبنای باینری است.
در ادامه برای مثال عدد 41 را به عدد معادل باینری آن تبدیل می کنیم.
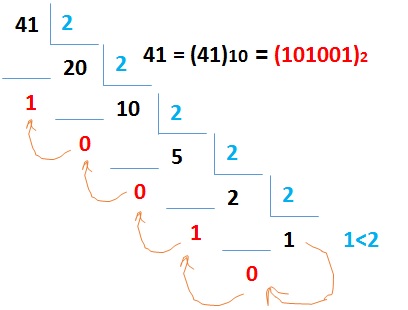
این روش کلی برای تبدیل یک عدد از مبنا 10 به مبنای دلخواهمان است و
می توان به جای عدد 2 هر مبنای دلخواه دیگری را قرار داد.
4# تبدیل عدد اعشاری به باینری
حالا اگر اعدادمان اعشاری بود، چه باید بکنیم؟
مثلا اگر عددمان 41/75 باشد
مبنای 2 آن را چگونه محاسبه می کنید؟
- قسمت صحیح عدد را به همان صورت قبلی به مبنای 2 می آوریم.
- برای قسمت اعشاری به جای تقسیم متوالی از ضرب های متوالی در عدد 2 استفاده میکنیم و
این روند را تا جایی پیش می بریم که عدد اعشاری مساوی 0 شود. - از اولین حاصل ضرب تا آخر بخش عدد صحیح جواب ها را به ترتیب پشت سر هم می نویسیم.
- عدد باینری حاصل از قسمت صحیح عدد را مشابه قبل نوشته و پس از قرار دادن یک نقطه (.) بخش اعشاری باینری رو مینویسیم.
در ادامه عدد 41/75 را به مبنای باینری می بریم.
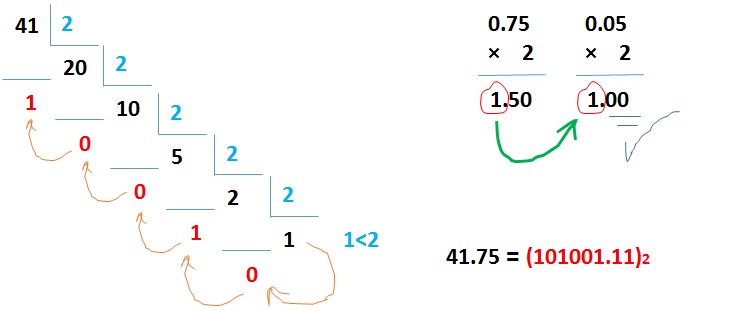
- قسمت اعشاری ممکن است، هیچ موقع به صفر نرسد
(مثلا برای 0.32 این اتفاق رخ می دهد و هرگز به صفر نمی رسد)
5# تبدیل اعداد باینری به دسیمال
در مبنای باینری، اعداد دارای ارزش گذاری مخصوص به خود هستند به این صورت که
از سمت راست ترین رقم عدد صحیح، عدد nام، دارای ارزش 2 به توان n-1 است.
یعنی از سمت راست، رقم اول ارزش 2 به توان 0 (یعنی 1) دارد، عدد دوم ارزش 2، سومین رقم ارزش 4 و الی آخر.
برای تبدیل این عدد به مبنای دسیمال کافی است هر رقم را در ارزش خودش ضرب کرده و حاصل ضرب ها را با هم جمع کنیم.
یه سمت راستی ترین رقم اعداد باینری که دارای کمترین ارزش مقداری است LSB گفته می شود و
به سمت چپ ترین رقم که دارای بیشترین ارزش مقداری است MSB می گویند.
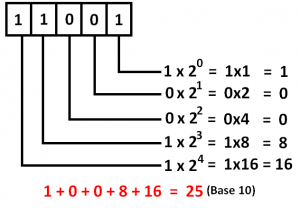
برای بخش اعشاری اعداد هم به همین روش پیش میرویم با این تفاوت که این بخش دارای ارزش های متفاوت است.
از سمت چپ ترین رقم، عدد nام دارای ارزش 2 به توان n- است.
برای مثال از سمت چپ به ترتیب دارای ارزش 2 به توان 1-، 2 به توان 2- و الی آخر خواهند بود.
6# روش سریع تبدیل مبنای اعداد
در این مرحله می خواهیم، میان بری برای تبدیل به مبنای دلخواهمان پیدا کنیم.
اگر به ارزش مکانی ارقام دقت کنید، می توانید تبدیل مبنا ها را سریع تر و دقیق تر انجام دهید.
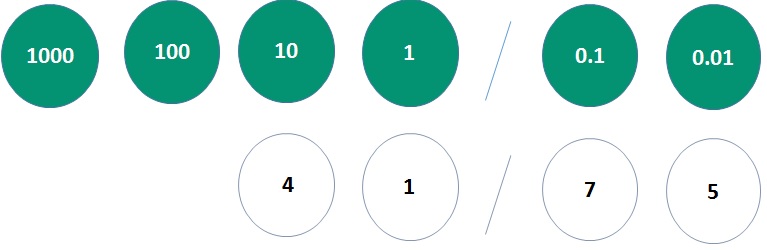
حالا اگر بخواهیم عدد 41.75 را با توجه به ارزش های مکانی در سیستم دودویی بنویسیم،
یا به عبارت بهتر به اعداد باینری تبدیل کنیم.

به ارزش مکانی اعداد باینری یا دودویی باید توجه کنیم.
همان طور که در تصویر فوق مشاهده می کنید، ارزش مکانی سیستم دودویی برای شما نمایش داده شده است.
ابتدا خودتان سعی کنید که به روش میان بر، مقدار دودویی عدد 41.75 را بدست بیاورید
(قرار است که عدد 0 و 1 را طوری زیر ارزش های مکانی دودویی بگذاریم که مجموع آنها با توجه به ارزش شان، 41.75 شود!)
- نزدیک ترین عدد کوچکتر از 41، عدد 32 است(1)
- مشخصا، 32+16>41 می شود! (0)
- اما 40=32+8<41 است و در ارزش مکانی 8، از رقم 1 استفاده می کنیم (1)
- سپس 40+4>41 است (0)
- و 40+2>41 است و همان رقم 0 را برای ارزش مکانی 2 در نظر می گیریم (0)
- و در انتها 40+1=41 و تمام (1)
- ارقام فوق را به ترتیب وارد می کنیم
برای قسمت اعشاری هم داریم:
- 1/2>0.75 است (1)
- همچنین 1/2+1/4=0.75 است و برای این ارزش مکانی هم رقم 1 را در نظر می گیریم و تمام

خیلی ساده مشاهده کردید که رقم 41.75 را با سرعت بیشتری به سیستم دودویی تبدیل کردیم (101001.11)
و به همان جواب قبلی رسیدیم.
7# جمع اعداد باینری
جمع اعداد باینری بسیار ساده و مشابه جمع اعداد در مبنای دهدهی است.
از سمت راست دو رقم، دو رقم با هم جمع کرده و رقم نقلی (Carry) اضافه را به رقم بعدی منتقل میکنیم و
سپس با انها جمع میکنیم.
برای جمع اعداد باینری به صورت زیر باید عمل کنیم:
0+0 = 0
0+1 = 1
1+1 = 0 , مقدار رقم نقلی 1 است.
1+1+1 = 1 , مقدار رقم نقلی 1 است.
به مثال زیر توجه کنید:
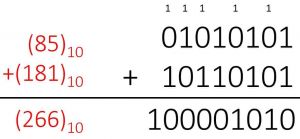
8# تفریق دو اعداد باینری
برای تفریق دو عدد باینری کافی است، مکمل دو عدد دوم را محاسبه کنیم و با عدد اول جمع کنیم.
9# مکمل دوم عدد باینری
برای محاسبه مکمل دوم یک عدد باینری، لازم است مکمل اول عدد را محاسبه کنیم و
با یک جمع کنیم.
مکمل اول یک عدد باینری به این صورت محاسبه می شود که
هر عدد 0 را به 1 و هر عدد 1 را به صفر تبدیل میکنیم.
برای مثال مکمل اول عدد، 010010 مساوی مقدار 101101 است.
برای محاسبه مکمل دوم این عدد را با 1 جمع میکنیم که می شود: 101110
یک روش ساده تر برای محاسبه مکمل دو وجود دارد که ادامه توضیح میدهیم.
کافی است از سمت راست تمامی صفرها و اولین 1 را رها کرده و سپس الباقی اعداد را مثل مکمل یک تغییر دهیم.
در همان مثال بالا از سمت راست اولین 0 و 1 را جدا کرده و از رقم سوم تغییر میدهیم که
مساوی مقدار 101110 می شود.
10# جمع و تفریق اعداد باینری با ماشین حساب
همین الان دکمه پنجره کیبورد خود را بزنید و در قسمت جستجو calculator را تایپ کنید:
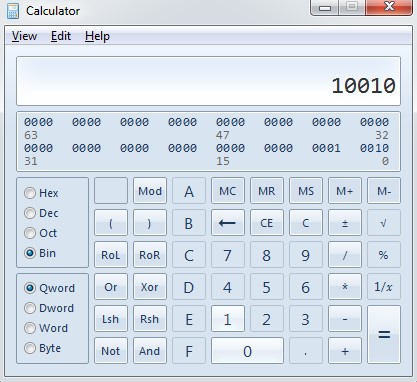
در تگ view، گزینه programmer را انتخاب کنید.
حالا قادر خواهید بود که اعداد را از باینری به دسیمال و .. تبدیل کرده و همچنین به جمع و تفریق اعداد باینری بپردازید.
یکی از اساسی ترین کاربردهای اعداد باینری به صورت فیزیکی در گیت های الکترونیکی است که
خودشان پایه و اساس الکترونیک دیجیتال هستند.
برای آشنایی با گیت های منطقی و طرز استفاده آن ها از اعداد باینری به مقاله مربوط به آن مراجعه کنید.
نظرتون درباره این مقاله چیه؟
ما رو راهنمایی کنید تا اون رو کامل تر کنیم و نواقصش رو رفع کنیم.
توی بخش دیدگاه ها منتظر پیشنهادهای فوق العاده شما هستیم.




با سلام و احترام
در مورد عدد ۰۰۳۲
در اعداد باینری کسری نوشته شده که هیچگاه به صفر نمی رسد خواهشمندم در صورت امکان توضیح فرمایید.با امتنان.
سلام همراه گرامی
طبق روش آموزش داده شده برخی از اعداد که در مبنای دهدهی اعشاری هستند در مبنای باینری هم اعشاری کامل می شوند؛ اما در این مبنا هم مانند اعداد دسیمال یا همان دهدهی ممکن است یک عدد اعشاری کامل به دست نیاید و تعداد زیادی رقم اعشار خواهد داشت.
این اتفاق در اعداد دهدهی هم می افتد و اصطلاحا می گوییم یک عدد دارای اعشار با دور گردش است برای مثال تقسیم عدد ۱۰۰ بر ۳ مقدار ۳۳.۳۳۳۳۳۳ را می دهد و این عدد هرگز یک اعشار کامل نخواهد داشت و دور گردش ۳ دارد.
در تبدیل عدد ۰.۳۲ به باینری هم همین اتفاق رخ می دهد.
موید باشید
واقعاً خیلی عالی بود
سلام همراه محترم
سپاس از لطف و مهربانی شما
خرسندیم که این مطلب برای شما رضایت بخش بوده
موفق باشید
عالی متشکر
سلام همراه گرامی
ممنون از محبت تون
سلام
به چه روشی عدد دیسیمال اعشاری رو به عدد باینری عشاری تبدیل کنیم و برعکس و برعکس
سلام خدمت شما مهندس بزرگوار
لطفا سوالات تخصصی خودتان را در فروم سایت به ادرس لینک زیر مطرح بفرمایید تا عزیزان راهنمایی کنند
https://katibeha.com
از همراهی شما با تیم نماتک سپاسگزاریم.
واقعا عالی بود
مهندس گودینی بسیار عالی توضیح دادند.
سلام خدمت شما دوست عزیز
از لطف و محبت شما سپاسگزار هستیم و خرسندیم که مطالب سایت برای شما مفید واقع شده.
ممنون از همراهی شما با سایت نماتک
موفق و پیروز باشید.
سلام ،،،، خیلی خوب بود ،،،،،،، اگه ویدئو باشه توضیحات عالیییی میشه ،،،، سپاس
سلام خدمت شما بزرگوار
ممنون از لطف و محبت شما به تیم نماتک
از همراهی شما با تیم نماتک سپاسگزاریم
موفق و موید باشید
با سلام
تفریق اعداد باینری رو توضیح میدین🙏🏻🌹
سلام خدمت شما بزرگوار
داخل متن مقاله به طور کامل توضیح داده شده لطفا مطالعه بفرمایید
از همراهی شما با تیم نماتک سپاسگزاریم
موید باشید
سلام عرض ادب و احترام به مدیریت محترم سایت و مسعول نماتک
اینجانب بهاری کارشناس برق از دانشگاه ازاد تهران هستم و پنجاه ساله هستم
و از ریاست محترم نماتک تشکر و قدر دانی میکنم که همیشه بهترین روش اموزش و اسان و دفیق و کامل و جامع و سریع را دارید و با تجربه و با دقت به کار بران اموزش میدهید امیدوارم که همیشه شاد تن درست و برقرار باشید انشا الله
سلام خدمت شما جناب امجد بزرگوار
از لطف و محبت شما به تیم نماتک بسیار سپاسگزاریم
بودن شما همراهان عزیز در این راه باعث قوت قلب ما هست
موفق و موید باشید
عالی بود
سلام جناب محمودی
ممنون از همراهی شما
پیروز باشید
سلام ببخشید تفاضل ۱۰۱۱۱۰۱ از ۱۱۰۰۰۱۱ چند میشه ؟ من حساب میکنم ولی فک میکنم جوابم اشتباهه میشه لطفا بگید مکلمش و جواب اخرش چند میشه
سلام وقت بخیر
دوست عزیز ممنون میشم لطف کنین سوال های تخصصی و فنی تون رو در بخش پرسش و پاسخ سایت مطرح بفرمایید
katibeha.com
عالیی
سایتتون عالیه
سلام جناب شجاعیان
سپاس از محبتی که به ما دارید
سربلند باشید
خدا خیرت بده👍
سلام مهندس
ممنون از محبتتون
موید باشید
سلام
لطفا توضیح دهید چگونه دستی ۱۱۰۰۰۱۰۰را منهای ۱۱۰۱۱ کنیم. جواب میشه ۱۰۱۰۱۰۰۱ اما دستی با روش مکمل ۲ که گفتید بدست نمیاد. نکته اش کجاست؟ ممنونم
سلام
برای این تفاضل کافیه مکمل دو عدد دوم رو زمانی بدست بیارید که براساس تعداد رقم های اول ۰ پشتش گذاشته شده.
یعنی عدد دوم در اصل ۰۰۰۱۱۰۱۱ هست که بعد از مکمل دو گیری میشه ۱۱۱۰۰۱۰۱ و حالا جمع این عدد با عدد قبلی میشه همون مقداری که فرمودید.
موفق باشید
سلام
لطفا توضیح دهید
چند کد وزنی و خود مکمل با ارزش های ۱، ۲، ۲، ۴ وجود دارد؟
و همچنین روشی برای جمع و تفریق دودویی اعدادی که با سیستم ex-3و BCD 6 کد شدند،هست؟
سلام
لطفا سوالات تخصصی خودتون در فروم نماتک مطرح کنید.
katibeha.com