انواع توزیع های آماری و کاربردهای آن ها

در دنیای پیچیده و متغیر امروز، داده‌ها به عنوان ستون‌های اطلاعاتی جوامع مدرن شناخته می‌شوند.

اما چگونه می‌توان از این حجم عظیم داده‌ها، دانش و بینشی معتبر استخراج کرد؟

پاسخ این پرسش در درک عمیق از توزیع‌های آماری نهفته است.

توزیع‌های آماری، همچون زبانی مشترک بین رشته‌های مختلف، امکان تفسیر و تحلیل داده‌ها را فراهم می‌آورند و به ما اجازه می‌دهند تا با دقتی بیشتر به پیش‌بینی پدیده‌های آتی بپردازیم.

در این مقاله، ما انواع توزیع های آماری را بررسی خواهیم کرد، از توزیع‌های گسسته که در قلب شمارش و احتمالات قرار دارند، تا توزیع‌های پیوسته که دنیای بی‌انتهای اعداد را در بر می‌گیرند.

همراه ما باشید.

1# توزیع آماری چیست؟

توزیع آماری، که به عنوان نقشه‌ای از احتمالات شناخته می‌شود، به ما می‌گوید که یک متغیر تصادفی چگونه مقادیر مختلف خود را در یک مجموعه از داده‌ها توزیع می‌کند.

این توزیع‌ها می‌توانند به دو دسته کلی گسسته و پیوسته تقسیم شوند.

توزیع‌های گسسته، مانند توزیع برنولی یا دوجمله‌ای، زمانی استفاده می‌شوند که متغیر تصادفی مقادیری را اتخاذ می‌کند که قابل شمارش هستند.

در مقابل، توزیع‌های پیوسته، مانند توزیع نرمال یا اکسپوننشیال (Exponential)، برای متغیرهایی به کار می‌روند که می‌توانند هر مقداری در یک بازه مشخص بگیرند.

به طور خلاصه، انواع توزیع های آماری به ما اطلاعاتی در مورد اینکه چگونه داده‌ها در میان مقادیر مختلف پراکنده شده‌اند و هر مقدار چه احتمالی دارد، می‌دهند.

این اطلاعات برای تحلیل داده‌ها و انجام پیش‌بینی‌های آماری بسیار حیاتی هستند.

2# اهمیت توزیع های آماری

انواع توزیع های آماری ابزارهای قدرتمندی در علم آمار و تجزیه و تحلیل داده‌ها هستند که به ما امکان می‌دهند تا شکل و رفتار کلی یک مجموعه داده را توصیف کنیم.

این توزیع‌ها به ما کمک می‌کنند تا الگوها، روندها و نقاط پرت را در داده‌ها شناسایی کنیم و پیش‌بینی‌های دقیق‌تری انجام دهیم.

درک توزیع‌های آماری به ما این امکان را می‌دهد که:

• الگوها و روندها را در داده‌ها شناسایی کنیم: توزیع‌های آماری به ما نشان می‌دهند که داده‌ها چگونه در اطراف میانگین یا مد متمرکز شده‌اند و چه توزیع فراوانی دارند.
• پیش‌بینی‌های دقیق‌تری انجام دهیم: با شناخت توزیع زیربنایی داده‌ها، می‌توانیم احتمال وقوع رویدادهای آینده را بهتر پیش‌بینی کنیم.
• قابلیت اطمینان یافته‌های خود را ارزیابی کنیم: توزیع‌های آماری به ما کمک می‌کنند تا درک کنیم که چقدر می‌توانیم به نتایج تحلیل‌های خود اعتماد کنیم.
• آزمون‌ها و مدل‌های آماری مناسبی را انتخاب کنیم: با شناخت توزیع داده‌ها، می‌توانیم مدل‌ها و آزمون‌های آماری را انتخاب کنیم که با داده‌های ما متناسب باشند.

به طور خلاصه، تسلط بر توزیع‌های آماری به ما این امکان را می‌دهد که از داده‌های خود بیشترین استفاده را ببریم و بینش‌های معناداری را به دست آوریم که می‌تواند در تصمیم‌گیری‌های آگاهانه‌تر و بهبود عملکرد کسب‌وکارها و تحقیقات علمی مؤثر باشد.

3# انواع توزیع های آماری متغیرهای تصادفی گسسته

متغیرهای تصادفی گسسته مقادیری را اتخاذ می‌کنند که قابل شمارش و محدود هستند.

این مقادیر می‌توانند شامل تعداد دفعات وقوع یک رویداد، تعداد اشیا در یک مجموعه یا هر مقدار دیگری که به صورت عدد صحیح بیان می‌شود، باشند.

در ادامه، به برخی از مهم‌ترین توزیع‌های متغیرهای تصادفی گسسته می‌پردازیم.

1-3# توزیع برنولی

این توزیع برای مدل‌سازی آزمایش‌هایی با دو نتیجه ممکن، مانند موفقیت یا شکست، استفاده می‌شود.

مثال کلاسیک آن پرتاب سکه است که می‌تواند شیر یا خط بیفتد.

توزیع برنولی یک توزیع احتمال گسسته است که فقط دو مقدار ممکن دارد: 1 (برای موفقیت) و 0 (برای شکست).

تابع احتمال متغیر تصادفی برنولی به صورت زیر است:

P (X = x) = p^x (1-p)^(1-x)

که در آن (x) مقادیر 0 یا 1 را می‌گیرد.

2-3# توزیع دوجمله‌ای

توزیع دوجمله‌ای، که تعمیمی از توزیع برنولی است، تعداد دفعات موفقیت در (n) آزمایش مستقل را مدل‌سازی می‌کند.

این توزیع برای مواردی که می‌خواهیم تعداد دفعات وقوع یک رویداد خاص را در یک تعداد آزمایش مشخص بدانیم، کاربرد دارد.

توزیع دوجمله‌ای یک توزیع احتمال گسسته است که تعداد موفقیت‌ها در یک سلسله آزمایش‌های برنولی مستقل با احتمال موفقیت ثابت (p) را مدل می‌کند.

اگر (X) تعداد موفقیت‌ها در (n) آزمایش برنولی باشد، آنگاه (X) دارای توزیع دوجمله‌ای با پارامترهای (n) و (p) است و به صورت X ∼ B(n, p) نمایش داده می‌شود.

تابع احتمال برای متغیر تصادفی دوجمله‌ای به صورت زیر است:

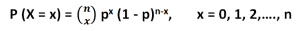
که در آن P(X = x) تعداد راه‌های انتخاب (x) موفقیت از (n) آزمایش است و (x) می‌تواند هر عدد صحیحی از 0 تا n باشد.

3-3# توزیع پواسون

توزیع پواسون برای مدل‌سازی تعداد رویدادهایی که در یک بازه زمانی یا فضایی مشخص رخ می‌دهند، استفاده می‌شود.

این توزیع زمانی کاربرد دارد که احتمال وقوع رویداد در هر نقطه از زمان یا فضا بسیار کم باشد.

توزیع پواسون معمولاً برای شمارش تعداد رویدادهای نادر در یک فاصله زمانی یا مکانی مشخص به کار می‌رود، مانند تعداد تماس‌های دریافتی در یک مرکز تلفن در یک ساعت یا تعداد خطاهای چاپی در یک صفحه کتاب.

اگر (X) تعداد رویدادهایی باشد که در یک بازه زمانی یا مکانی مشخص رخ می‌دهند و اگر λ نرخ میانگین رویدادها در واحد زمان یا مکان باشد، آنگاه (X) دارای توزیع پواسون با پارامتر (λ) است.

تابع جرم احتمال برای متغیر تصادفی پواسون به صورت زیر است:

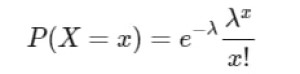
که در آن (x) تعداد رویدادها (معمولاً عدد صحیح) و (e) پایه لگاریتم طبیعی (تقریباً برابر با 2.71828) است.

4-3# توزیع هندسی

توزیع هندسی تعداد آزمایش‌های لازم برای رسیدن به اولین موفقیت را مدل‌سازی می‌کند.

این توزیع در مواردی که می‌خواهیم بدانیم چه تعداد تلاش لازم است تا به اولین موفقیت برسیم، مفید است.

توزیع هندسی یک توزیع احتمال گسسته است که تعداد آزمایش‌های لازم برای رسیدن به اولین موفقیت در یک سلسله آزمایش‌های برنولی مستقل با احتمال موفقیت ثابت (p) را مدل می‌کند.

اگر (X) متغیر تصادفی باشد که تعداد آزمایش‌های لازم برای رسیدن به اولین موفقیت را نشان دهد، آنگاه (X) دارای توزیع هندسی است.

تابع جرم احتمال برای متغیر تصادفی هندسی به صورت زیر است:

⁽P(X = x) = p (1-p)^(x-1

که در آن (x) تعداد آزمایش‌های انجام شده تا رسیدن به اولین موفقیت است و مقادیر (x) از 1 شروع می‌شود.

این توزیع دارای خاصیت بی‌حافظگی است، به این معنی که احتمال رسیدن به اولین موفقیت در آزمایش (x+1)ام، به شرطی که تا آزمایش (x)ام موفقیتی حاصل نشده باشد، فقط به احتمال موفقیت (p) بستگی دارد و مستقل از (x) است.

به عبارت دیگر، احتمال رسیدن به اولین موفقیت در هر آزمایش بعدی، همان احتمال (p) است، صرف نظر از تعداد شکست‌های قبلی.

5-3# توزیع یکنواخت گسسته

در توزیع یکنواخت گسسته، هر یک از مقادیر ممکن متغیر تصادفی دارای احتمال یکسانی هستند.

مثالی از این توزیع، پرتاب یک تاس است که هر یک از شش وجه آن احتمال برابری برای ظاهر شدن دارند.

این توزیع معمولاً برای مدل‌سازی شرایطی استفاده می‌شود که در آن هر نتیجه‌ای از یک آزمایش تصادفی به طور یکسان محتمل است، مانند پرتاب یک تاس سالم.

اگر (X) یک متغیر تصادفی با تکیه‌گاه ( S = {1, 2, 3, …, n} ) باشد، که در آن (n) تعداد نتایج ممکن است، تابع جرم احتمال برای توزیع یکنواخت گسسته به صورت زیر است:

P(X = x) = 1/n

برای هر (x) در تکیه‌گاه (S)1.

این توزیع دارای خصوصیات زیر است:

• میانگین (امید ریاضی) و میانه توزیع یکنواخت گسسته برابر است با 2 / (n+1)
• واریانس (پراکندگی) آن برابر است با 12/(n² – 1)
• تابع توزیع تجمعی F(x) برای متغیر تصادفی یکنواخت گسسته به صورت زیر است:

FX(x) = P(X ≤ x) = [x]/n

برای (x) در تکیه‌گاه (S) که در آن [x] بزرگترین عدد صحیح کوچکتر یا مساوی (x) است.

4# انواع توزیع های آماری متغیرهای تصادفی پیوسته

متغیرهای تصادفی پیوسته در مقابل متغیرهای گسسته، مقادیری را اتخاذ می‌کنند که در یک بازه مشخص، نامتناهی و غیرقابل شمارش هستند.

این مقادیر می‌توانند شامل مساحت، وزن، زمان یا هر مقدار دیگری که به صورت عدد حقیقی بیان می‌شود، باشند.

در ادامه، به برخی از مهم‌ترین توزیع‌های متغیرهای تصادفی پیوسته می‌پردازیم.

1-4# توزیع نرمال

شاید معروف‌ترین توزیع پیوسته، توزیع نرمال یا گاوسی باشد که به دلیل شکل زنگی خود به توزیع زنگوله‌ای نیز معروف است.

این توزیع برای مدل‌سازی داده‌هایی که دور میانگین متمرکز شده‌اند و انحراف معیار مشخصی دارند، استفاده می‌شود.

توزیع نرمال، که به آن توزیع گاوسی نیز گفته می‌شود، یکی از مهم‌ترین توزیع‌های احتمالی پیوسته در نظریه احتمالات است.

این توزیع برای مدل‌سازی پدیده‌هایی که داده‌های آن‌ها حول یک میانگین مرکزی توزیع شده‌اند، استفاده می‌شود.

توزیع نرمال به دلیل شکل زنگوله‌ای منحنی تابع چگالی احتمالش شناخته شده است و بسیاری از پدیده‌های طبیعی و اجتماعی را توصیف می‌کند.

تابع چگالی احتمال برای توزیع نرمال به صورت زیر است:

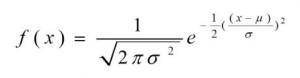
که در آن:

• (x) متغیر تصادفی است.
• (μ) میانگین توزیع است.
• (σ) انحراف معیار توزیع است.
• (σ²) واریانس توزیع است.

توزیع نرمال دارای خصوصیات زیر است:

• میانگین، میانه و مُد همگی برابر با (μ) هستند.
• تابع چگالی احتمال شکل زنگوله‌ای دارد و حول میانگین متقارن است.
• انحراف معیار (σ) پهنای زنگوله را تعیین می‌کند و نشان‌دهنده پراکندگی داده‌ها حول میانگین است.

2-4# توزیع یکنواخت پیوسته

در توزیع یکنواخت پیوسته، هر یک از مقادیر در یک بازه مشخص دارای احتمال یکسانی هستند.

این توزیع برای مدل‌سازی پدیده‌هایی که در آن‌ها هر نتیجه‌ای به طور یکسان محتمل است، مناسب است.

فرمول محاسبه تابع توزیع یکنواخت پیوسته به صورت زیر است:

F(x) = 1/(b-a) برای x های مابین a و b  

F(x) = 0 برای x های کمتر از a و بیشتر از b

3-4# توزیع اکسپوننشیال

توزیع اکسپوننشیال برای مدل‌سازی زمان انتظار تا وقوع اولین رویداد در یک فرآیند پواسون استفاده می‌شود.

این توزیع در مواردی که رویدادها به صورت ناپیوسته و با نرخ ثابت رخ می‌دهند، کاربرد دارد.

توزیع اکسپوننشیال یک توزیع احتمال پیوسته است که برای مدل‌سازی زمان انتظار تا وقوع اولین رویداد در یک فرآیند پواسون به کار می‌رود.

این توزیع برای توصیف زمان بین رویدادهایی که به صورت مستقل و با نرخ ثابت رخ می‌دهند، استفاده می‌شود، مانند زمان بین تماس‌های ورودی در یک مرکز تلفن یا زمان بین وقوع حوادث در یک فرآیند شیمیایی.

اگر (X) متغیر تصادفی باشد که زمان انتظار تا وقوع اولین رویداد را نشان دهد و (λ) نرخ میانگین وقوع رویداد در واحد زمان باشد، آنگاه (X) دارای توزیع اکسپوننشیال با پارامتر (λ) است.

تابع چگالی احتمال برای توزیع اکسپوننشیال به صورت زیر است:

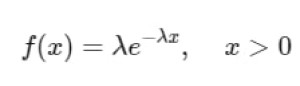
توزیع اکسپوننشیال دارای خاصیت بی‌حافظگی است، به این معنی که احتمال وقوع اولین رویداد در زمان (t + s) به شرطی که تا زمان (t) رویدادی رخ نداده باشد، فقط به (s) بستگی دارد و مستقل از (t) است.

3-4# توزیع گاما

توزیع گاما تعمیمی از توزیع اکسپوننشیال است و برای مدل‌سازی زمان انتظار تا وقوع (k) رویداد در یک فرآیند پواسون به کار می‌رود.

توزیع گاما یک توزیع احتمال پیوسته است که دارای دو پارامتر، پارامتر شکل (k) و پارامتر مقیاس (θ) می‌باشد.

این توزیع برای مدل‌سازی زمان انتظار برای وقوع (k) رویداد در فرآیندهایی که رویدادها به صورت مستقل و با نرخ ثابت رخ می‌دهند، استفاده می‌شود.

برای مثال، اگر (k) عددی طبیعی باشد، توزیع گاما معادل است با مجموع (k) متغیر تصادفی با توزیع نمایی.

تابع چگالی احتمال برای توزیع گاما به صورت زیر است:

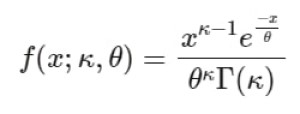
که در آن (x) مقادیر بزرگتر یا مساوی صفر را می‌گیرد و (Γ) تابع گاما برای پارامتر شکل (k) است.

4-4# توزیع بتا

توزیع بتا برای متغیرهای تصادفی که مقادیرشان بین 0 و 1 قرار دارند، مناسب است.

این توزیع در مواردی که داده‌ها نسبت‌ها یا درصدهایی هستند که در یک بازه محدود قرار دارند، استفاده می‌شود.

توزیع بتا یک توزیع احتمال پیوسته است که بر بازه [0, 1] تعریف می‌شود و دارای دو پارامتر مثبت (α) و (β) است.

این توزیع برای مدل‌سازی متغیرهای تصادفی محدود به بازه‌ای خاص، مانند نسبت‌ها یا درصدها، استفاده می‌شود.

تابع چگالی احتمال برای توزیع بتا به صورت زیر است:

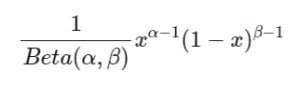
که در آن Beta (α, β) نسبت دو مقدار تابع گاما است.

5# تفاوت بین متغیر تصادفی گسسته و پیوسته

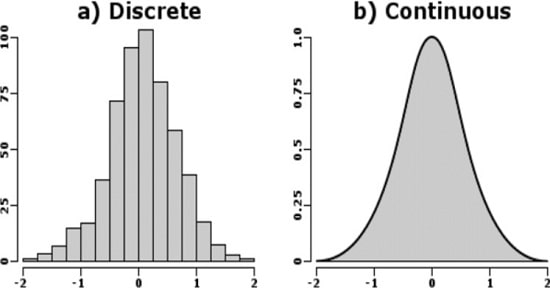
همانطور که بررسی کردیم، انواع توزیع های آماری متغیرهای تصادفی در دو دسته کلی گسسته و پیوسته قرار می‌گیرند که هر کدام ویژگی‌های منحصر به فردی دارند:

• متغیر تصادفی گسسته: این نوع متغیر مقادیری را اتخاذ می‌کند که قابل شمارش هستند.
  به عبارت دیگر، مقادیری که متغیر تصادفی گسسته می‌تواند بگیرد، محدود یا شمارش پذیر بی‌نهایت است.
  مثال‌هایی از این نوع متغیر شامل تعداد افراد در یک کلاس، تعداد دفعات پرتاب سکه که شیر می‌آید یا تعداد خودروهای فروخته شده توسط یک نمایندگی در یک روز می‌باشد.
• متغیر تصادفی پیوسته: متغیرهای تصادفی پیوسته مقادیری را می‌پذیرند که در یک بازه مشخص، نامحدود و غیرقابل شمارش هستند.
  این مقادیر می‌توانند هر عدد حقیقی در آن بازه باشند، مانند وزن یا قد یک فرد، فاصله طی شده توسط یک خودرو یا زمان انتظار برای خدمات مشتری.

به طور خلاصه، تفاوت اصلی بین این دو نوع متغیر در نوع مقادیری است که می‌توانند بگیرند.

6# کاربردهای انواع توزیع های آماری

انواع توزیع های آماری در بسیاری از زمینه‌های علمی و کاربردی مورد استفاده قرار می‌گیرند و نقش مهمی در تحلیل داده‌ها و پیش‌بینی رویدادها دارند.

در اینجا به برخی از کاربردهای مهم توزیع‌های آماری اشاره می‌کنیم:

• علوم داده و داده کاوی: توزیع‌های آماری برای شناسایی الگوها و تحلیل رفتار داده‌ها در حوزه‌های مختلف علوم داده استفاده می‌شوند.
• مهندسی و کنترل کیفیت: در مهندسی، توزیع‌های آماری برای ارزیابی کنترل فرآیندها و تضمین کیفیت محصولات به کار می‌روند.
• اقتصاد و تجارت: توزیع‌های آماری در تجزیه و تحلیل بازارهای مالی و پیش‌بینی روندهای اقتصادی نقش دارند.
• علوم اجتماعی: در علوم اجتماعی، توزیع‌های آماری برای مطالعه رفتارهای جمعی و پدیده‌های اجتماعی مورد استفاده قرار می‌گیرند.
• پزشکی و بیولوژی: توزیع‌های آماری برای تحلیل داده‌های پزشکی و بیولوژیکی و همچنین برای طراحی و تحلیل آزمایش‌های بالینی به کار می‌روند.
• فیزیک و شیمی: در فیزیک و شیمی، توزیع‌های آماری برای مدل‌سازی پدیده‌های فیزیکی و شیمیایی و تحلیل نتایج آزمایش‌ها استفاده می‌شوند.

این کاربردها نشان‌دهنده اهمیت و گستردگی استفاده از توزیع‌های آماری در تحلیل و پیش‌بینی پدیده‌های مختلف هستند و به ما کمک می‌کنند تا دنیای پیرامون خود را بهتر درک کنیم و تصمیمات آگاهانه‌تری بگیریم.

7# انتخاب توزیع مناسب

انتخاب انواع توزیع های آماری مناسب برای داده‌ها یکی از مهم‌ترین قدم‌ها در تحلیل آماری است.

این انتخاب بر اساس نوع داده‌ها، هدف تحلیل و پیش‌فرض‌های مربوط به توزیع‌های مختلف صورت می‌گیرد.

در ادامه به برخی از فاکتورهای تأثیرگذار در انتخاب توزیع آماری مناسب اشاره می‌کنیم:

• نوع داده‌ها: داده‌ها می‌توانند گسسته یا پیوسته باشند و این تفاوت در انتخاب توزیع نقش دارد.
• شکل توزیع داده‌ها: برخی داده‌ها ممکن است توزیع نرمال داشته باشند، در حالی که برخی دیگر ممکن است توزیعی نامتقارن یا توزیعی با دنباله‌های سنگین داشته باشند.
• پیش‌فرض‌های آماری: برخی آزمون‌های آماری نیازمند فرضیه توزیع نرمال هستند و درصورتی‌که این فرضیه برقرار نباشد، آزمون‌های غیرپارامتریک معمولاً مناسب‌تر هستند.
• هدف تحلیل: اهداف مختلف تحلیل ممکن است نیاز به توزیع‌های مختلف داشته باشند.
  برای مثال، تحلیل‌های پیش‌گویی ممکن است نیاز به توزیع‌هایی با خصوصیات خاص داشته باشند.
• آزمون‌های سازگاری: آزمون‌هایی مانند آزمون کولموگروف-اسمیرنوف، آزمون شاپیرو-ویلک و آزمون اندرسون-دارلینگ می‌توانند برای بررسی سازگاری داده‌ها با توزیع‌های مختلف استفاده شوند.

انتخاب توزیع مناسب برای داده‌ها می‌تواند تأثیر قابل توجهی بر نتایج تحلیل آماری داشته باشد و به همین دلیل، این انتخاب باید با دقت و توجه به جزئیات داده‌ها و هدف تحلیل صورت گیرد.

نتیجه‌گیری

انواع توزیع های آماری ابزارهای بسیار مهمی در تحلیل داده‌ها هستند که به ما امکان می‌دهند تا پدیده‌های تصادفی را درک کنیم و در مورد آن‌ها پیش‌بینی‌های دقیق انجام دهیم.

این توزیع‌ها به ما کمک می‌کنند تا الگوهای موجود در داده‌ها را شناسایی کنیم و به تفسیر و تحلیل آن‌ها بپردازیم.

از طریق استفاده از توزیع‌های مناسب، می‌توانیم به نتایجی برسیم که برای تصمیم‌گیری‌های آگاهانه و اقدامات مؤثرتر در زمینه‌های مختلف علمی، مهندسی، اقتصادی و اجتماعی حیاتی هستند.

با توجه به تنوع و پیچیدگی پدیده‌های تصادفی، انتخاب توزیع آماری مناسب می‌تواند چالش‌برانگیز باشد.

اما با درک صحیح داده‌ها و استفاده از روش‌های آماری معتبر، می‌توانیم از این توزیع‌ها به نحو احسن استفاده کنیم تا به درک عمیق‌تری از جهان پیرامون خود دست یابیم و آینده‌ای بهتر را شکل دهیم.

اگر به دنبال یاد گرفتن مهارت بیشتر و افزایش درآمد هستید،

برای دریافت آموزش های رایگان مرتبط با حوزه علاقه‌مندی خود فقط کافیه فرم رو تکمیل کنید.

نظرتون درباره این مقاله چیه؟
ما رو راهنمایی کنید تا اون رو کامل تر کنیم و نواقصش رو رفع کنیم.
توی بخش دیدگاه ها منتظر پیشنهادهای فوق العاده شما هستیم.