توزیع احتمال نرمال یا گوسی چیست؟

یکی از پراستفاده ترین توابع احتمالی، توزیع احتمال نرمال است که به دلیل شکل ظاهری آن به توزیع گوسی یا زنگوله ای نیز معروف است.

در قرن 19 ام میلادی انتشارات علمی منتشر شد که نشان می داد بسیاری از پدیده های طبیعی با این تابع توزیع رخ می دهند و دلیل نام گذاری آن به تابع نرمال هم همین علت است.

در این مقاله قصد داریم به بررسی توزیع احتمال نرمال، توزیع احتمال نرمال استاندارد، پارامترهای توزیع احتمال نرمال، ویژگی های توزیع احتمال نرمال و علل اهمیت آن بپردازیم.

1# توزیع احتمال نرمال چیست؟

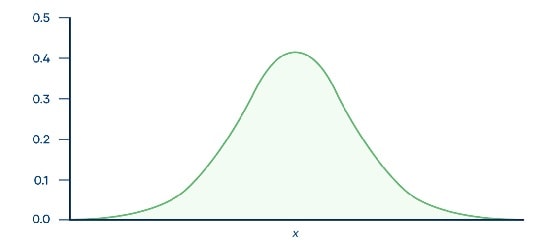
توزیع احتمال نرمال، مهمترین توزیع احتمال در آمار و برای متغیرهای تصادفی مستقل است.

این تابع یک توزیع احتمال پیوسته است که حول میانگین خود به صورت متغیر قرار دارد؛
تعداد زیادی از مشاهدات در اطراف قله مرکزی جمع می شوند و احتمالات برای مقادیر دورتر از میانگین به صورت مساوی و در دو جهت کاهش می یابند.

توزیع احتمال نرمال دارای موارد زیر است:

• مد = میانه = میانگین است.
• در مرکز نمودار، تقارن وجود دارد.
• 50 درصد موارد کمتر و 50 درصد موارد بیشتر از مقادیر میانگین هستند.

1-1# مثالی از توزیع احتمال نرمال

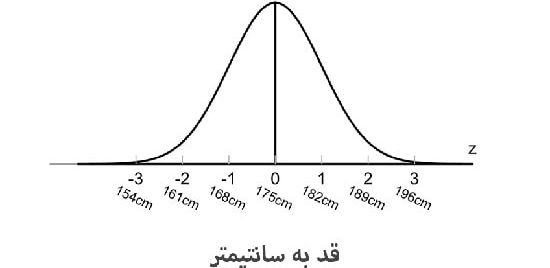
به عنوان مثال، متوسط قد انسان با احتساب زن و مرد بودن تقریباً 175 سانتیمتر است.

همانگونه که در نمودار بالا می بینید، اکثر مردم دارای قدی در حدود 175 سانتیمتر هستند.

افرادی که قد کوتاه تر یا بلندتر از مقدار میانگین دارند، فراوانی کمتری در جامعه دارند.

طبق قانون تجربی، حدود 99.7 درصد از تمامی افراد این جامعه دارای 3 انحراف معیار مثبت و منفی از میانگین یا بین 154 سانتیمتر تا 196 سانتیمتر هستند.

قدهایی بلندتر و کوتاه تر از این میزان معمولاً نادر هستند و تنها در حدود 0.15 درصد از جامعه را تشکیل می دهند.

2-1# توزیع احتمال نرمال استاندارد چیست؟

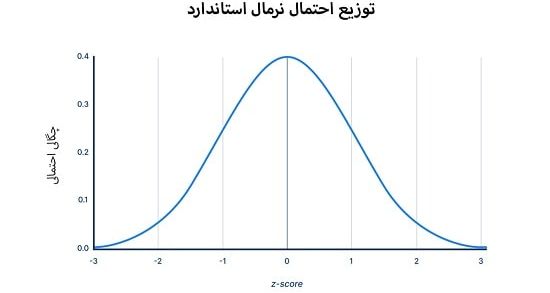
توزیع احتمال نرمال استاندارد که توزیع z نیز نامیده می شود، یک توزیع نرمال و ویژه است که میانگین آن صفر و انحراف معیار آن یک است.

هر توزیع نرمال، نسخه ای از توزیع نرمال استاندارد است که کشیده یا فشرده شده است و به صورت افقی به سمت راست یا چپ حرکت می کند.

در حالی که مشاهدات فردی از توزیع نرمال، x نامیده می شود؛ در توزیع استاندارد با عنوان z شناخته خواهد شد.

هر توزیع نرمال را می توان با تبدیل مقادیر فردی به z – score یا امتیاز z به توزیع نرمال استاندارد تبدیل کرد.

امتیاز z می گوید که هر مقدار به چه میزان انحراف استاندارد از میانگین، فاصله دارد.

در این حالت، کافی است که میزان میانگین و انحراف از استاندارد توزیع خود را بدانید تا بتوانید امتیاز z یک مقدار را به راحتی، محاسبه کنید.

فرمول z – score به صورت تصویر زیر است:

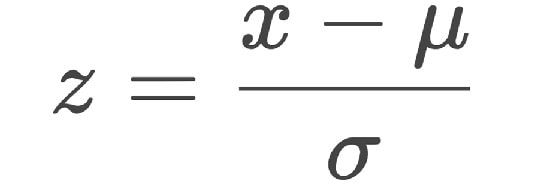
که پارامترهای آن عبارت اند از:

• x ارزش فردی
• μ میانگین
• σ انحراف معیار

بنابراین به منظور تبدیل یک مقدار به امتیاز استاندارد یا امتیاز z باید:

1. ابتدا میانگین را کم کنید.
2. سپس بر انحراف استاندارد تقسیم کنید.

انجام این مراحل، استانداردسازی نامیده می شود.

به چند دلیل بهتر است توزیع احتمال نرمال را به توزیع احتمال نرمال استاندارد تبدیل کرد:

• به منظور یافتن احتمال کاهش مشاهدات در یک توزیع، بیشتر یا کمتر از مقدار معین، استفاده می شود.
• به منظور به دست آوردن این که احتمال میانگین نمونه به صورت قابل توجهی با میانگین جامعه شناخته شده، متفاوت است.
• برای این که بتوان نمرات توزیع های مختلف را با میانگین ها و انحرافات استاندارد مختلف آن مقایسه کرد.

3-1# پارامترهای توزیع احتمال نرمال

توزیع احتمال نرمال دارای دو پارامتر اصلی است که عبارت اند از:

1. میانگین: 50 درصد از مقادیر بیشتر از مقدار میانگین و 50 درصد از آن ها کمتر از این مقدار خواهند بود.
2. انحراف معیار: معیاری برای سنجش میزان پراکندگی اعداد است و زمانی که انحراف از معیار را محاسبه می کنیم، متوجه مقادیری که در بخش قانون تجربی آمده است، خواهیم شد.

آمار، مدل نرمال میانگین و انحراف معیار را محاسبه می کند که شکل و احتمالات توزیع را مشخص می کند.

با تغییر مقادیر این پارامترها، شکل توزیع نیز تغییر خواهد کرد.

2# ویژگی های توزیع احتمال نرمال چیست؟

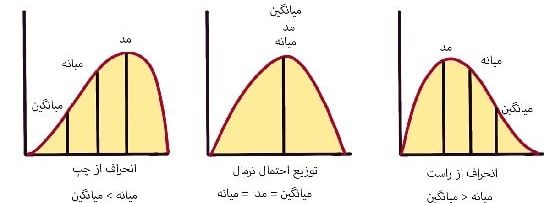
توزیع احتمال نرمال، دارای ویژگی های کلیدی است که به راحتی در نمودارها قابل تشخیص است.

این ویژگی ها به صورت زیر هستند:

• میانگین، میانه و مد دقیقاً یکسان هستند.
• توزیع نسبت به میانگین به صورت متقارن است، به این صورت که نیمی از مقادیر کمتر از مقدار میانگین و نیمی از آن ها بیشتر از آن هستند.
• میزان توزیع را می توان با استفاده از دو مقدار توصیف کرد که عبارت اند از:
  • میانگین: که پارامتر مکان است و تعیین می کند که نقطه اوج در کجا قرار می گیرد.
    با افزایش میانگین، منحنی به سمت راست حرکت می کند، در حالی که با کاهش آن، منحنی به سمت چپ حرکت خواهد کرد.
  • انحراف استاندارد: که پارامتر مقیاس است. انحراف معیار، منحنی را کشیده یا فشرده می کند.
    وجود یک انحراف استاندارد کوچک، منجر به ایجاد یک منحنی باریک خواهد شد؛ در حالی که وجود یک انحراف استاندارد بزرگ، منجر به ایجاد منحنی گسترده می شود.

در ادامه به بررسی سایر ویژگی ها و تعریف های توزیع احتمال نرمال می پردازیم.

1-2# قانون تجربی

قانون تجربی یا قانون 68 – 95 – 99.7 به شما می گوید که بیشترین مقادیر در کجای یک توزیع نرمال قرار گرفته اند:

• حدود 68 درصد از مقادیر، در یک انحراف استاندارد از میانگین قرار گرفته اند.
• در حدود 95 درصد از مقادیر، در 2 انحراف استاندارد از میانگین قرار دارند.
• حدود 99.7 درصد از مقادیر، در 3 انحراف استاندارد از میانگین قرار گرفته اند.

قانون تجربی، راهی سریع به منظور به دست آوردن یک دید کلی از داده های خود و بررسی مقادیر پرت یا شدیدی است که از این الگو پیروی نمی کنند.

اگر داده های مربوط به نمونه های کوچک دقیقاً از این الگو پیروی نکنند، توزیع های دیگری مانند توزیع t ممکن است، مناسب تر باشند.

هنگامی که توزیع متغیر خود را شناسایی کردید، می توانید آزمون های آماری مناسبی را اعمال کنید.

برای مثال می خواهید، نمرات SAT را در یک دوره آماده سازی آزمون جدید از دانش آموزان جمع آوری کنید.

داده ها از توزیع نرمال با میانگین امتیاز (M یا Mean Score) 1150 و انحراف معیار (Standard Deviation یا SD) 150 پیروی می کنند.

پس طبق قانون تجربی ما با آمار زیر رو به رو خواهیم بود:

• حدود 68 درصد از نمرات بین 1000 تا 1300 هستند که به میزان یک انحراف استاندارد بالاتر و پایین تر از میانگین است.
• حدود 95 درصد از نمرات بین 850 تا 1450 بوده که به میزان 2 انحراف استاندارد، بالاتر و پایین تر از حد میانگین خواهد بود.
• حدود 99.7 درصد از نمرات بین 700 تا 1600 است که به میزان 3 انحراف استاندارد از میانگین بیشتر و کمتر خواهد بود.

2-2# تئوری حد مرکزی

تئوری حد مرکزی، مبنایی برای نحوه عملکرد توزیع های نرمال در آمار است.

در تحقیقات و به منظور به دست آوردن یک ایده خوب از میانگین جامعه، در مد مناسب و ایده آل، داده ها را از چند نمونه تصادفی در جامعه، جمع آوری می کنند.

در توزیع نمونه گیری میانگین، توزیع میانگین این نمونه ها، مختلف و با یکدیگر متفاوت است.

قضیه حد مرکزی موارد زیر را نشان می دهد:

• قانون اعداد بزرگ به این صورت است که با افزایش حجم نمونه (یا تعداد نمونه ها)، میانگین نمونه به میانگین جامعه نزدیک می شود.
• با وجود چندین نمونه بزرگ، توزیع های نمونه گیری میانگین معمولاً توزیع خواهند شد، حتی اگر متغیر اصلی به صورت معمول، توزیع نشده باشد.

آزمون های آماری پارامتریک، معمولاً فرض می کنند که نمونه ها از جمعیت هایی با توزیع نرمال به دست می آیند؛ اما قضیه حد مرکزی به این معنا است که وقتی شما یک نمونه به اندازه کافی بزرگ دارید، وجود این چنین فرضی، ضروری نخواهد بود.

تا زمانی که سایر مفروضات مهم رعایت شوند، می توانید از آزمون های پارامتریک برای نمونه های بزرگی از جمعیت هایی با هر نوع توزیع استفاده کنید.

حجم نمونه با تعدادی در حدود 30 یا بیشتر معمولاً بزرگ در نظر گرفته می شود.

در نمونه های کوچک، فرض نرمال بودن مهم است؛ زیرا توزیع نمونه گیری میانگین، مشخص نیست.

به منظور به دست آوردن نتایج دقیق تر، قبل از این که بتوانید از آزمون های پارامتریک با نمونه های کوچک استفاده کنید، باید این اطمینان را به دست آورید که جامعه به صورت معمول توزیع شده باشد.

3-2# فرمول منحنی نرمال

هنگامی که میانگین و انحراف استاندارد یک توزیع نرمال در دسترس باشد، می توانید با استفاده از تابع چگالی احتمال، یک منحنی نرمال را با داده های خود سازگار کنید.

تابع چگالی احتمال، ناحیه ای که زیر منحنی احتمال وجود دارد را به شما نشان خواهد داد.

توزیع نرمال، یک توزیع احتمال است.

بنابراین مساحت کل زیر منحنی همیشه یک یا 100 درصد است.

فرمول تابع چگالی احتمال نرمال، نسبتاً پیچیده به نظر می رسد؛ اما به منظور استفاده از آن، فقط باید میانگین جمعیت و انحراف معیار را بدانید.

برای پیدا کردن هر مقدار از x می توان میانگین و انحراف استاندارد را به فرمول اضافه کرد تا چگالی احتمال متغیری که مقدار x را می گیرد را بتوان، به راحتی به دست آورد.

فرمول چگالی احتمال نرمال در تصویر زیر آمده است:

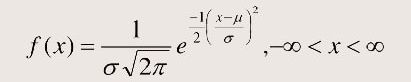
توضیح فرمول به صورت زیر است:

• F (x): احتمال
• X: متغیر

3# علل اهمیت توزیع احتمال نرمال چیست؟

تعداد زیاد و انواع مختلفی از متغیرها در علوم طبیعی و اجتماعی به صورت نرمال یا تقریباً نرمال توزیع شده اند:

• قد
• وزن
• تاریخ تولد
• توانایی خواندن
• رضایت شغلی

تنها چند نمونه از این متغیرها هستند.

از آنجایی که متغیرهایی که توزیع نرمالی دارند، بسیار رایج و متداول هستند، بسیاری از آزمون های آماری برای جمعیت هایی که توزیع نرمال دارند، طراحی شده اند.

درک ویژگی های توزیع نرمال بدین معنا است که می توان با استفاده از آمار استنباطی، مبادرت به مقایسه گروه های مختلف و ارائه تخمین هایی درباره جمعیت ها با توجه به نمونه های موجود کرد.

4# محدودیت های توزیع احتمال نرمال در امور مالی

اگرچه توزیع احتمال نرمال یک مفهوم آماری است؛ اما کاربردهای آن در امور مالی می تواند محدود باشد؛
زیرا پدیده های مالی مانند بازده مورد انتظار بازار سهام، به صورت منظم در توزیع احتمال نرمال قرار نمی گیرند.

قیمت ها در این حالت بیش از توزیع نرمال لگاریتم، با انتهای بزرگتر و ضخیم تر و به سمت راست می روند.

بنابراین اتکای بیش از حد به منحنی زنگ، هنگام پیش بینی می تواند منجر به نتایج غیر قابل اعتمادی شود.

اگرچه تحلیلگران به خوبی از وجود این چنین محدودیت هایی آگاه هستند، غلبه بر این مشکلات و نقص ها، بسیار دشوار است؛ زیرا اغلب مشخص نیست که از کدام توزیع آماری به عنوان جایگزین استفاده می شود.