سیستم مختصات در جغرافیا چیست؟ (بررسی ۷ نوع آن)

در دنیای پیچیده و دائماً در حال تغییر امروز، درک دقیق موقعیت‌ها و فضاها از اهمیت بالایی برخوردار است.

سیستم‌های مختصات، به عنوان ابزارهای بنیادین در جغرافیا، نقش کلیدی در نقشه‌برداری، ناوبری و تحلیل‌های مکانی ایفا می‌کنند.

این مقاله به بررسی جامع سیستم مختصات می‌پردازد و اهمیت آن‌ها را در زمینه‌های مختلف علمی و کاربردی تشریح می‌کند.

از سیستم‌های دکارتی گرفته تا سیستم‌های کروی، هر کدام نقش متمایزی در فهم و تفسیر دنیای اطراف ما دارند.

با پیشرفت‌های تکنولوژیکی و افزایش داده‌های مکانی، این سیستم‌ها بیش از پیش به ابزارهای ضروری در علوم جغرافیایی تبدیل شده‌اند. با ما همراه باشید.

1# سیستم مختصات در جغرافیا چیست؟

سیستم مختصات جغرافیایی یک سیستم سه‌بعدی کروی است که مکان‌ها را روی زمین تعریف می‌کند.

این سیستم برای اندازه‌گیری و ارتباط دادن موقعیت‌ها مستقیماً روی زمین به عنوان عرض و طول جغرافیایی استفاده می‌شود.

این سیستم، ساده‌ترین، قدیمی‌ترین و پرکاربردترین سیستم‌های مرجع فضایی است که در حال حاضر مورد استفاده قرار می‌گیرد.

همچنین پایه و اساس بیشتر سیستم‌های دیگر را تشکیل می‌دهد.

سیستم مختصات جغرافیایی از دو مختصه عرض و طول جغرافیایی تشکیل شده است که به صورت زاویه‌ای اندازه‌گیری می‌شوند و بر روی یک سطح صاف نیستند.

یک مشخصه کامل سیستم مختصات جغرافیایی، مانند آن‌هایی که در استانداردهای EPSG و ISO 19111 ذکر شده‌اند، شامل انتخاب داده‌های ژئودتیک (از جمله یک بیضی‌شکل زمین) نیز می‌شود؛ زیرا داده‌های مختلف می‌توانند مقادیر متفاوتی از عرض و طول جغرافیایی را برای یک مکان مشخص ارائه دهند.

این سیستم برای تعریف موقعیت ویژگی‌ها روی سطح زمین استفاده می‌شود.

همچنین امکان اندازه‌گیری فواصل و زوایا بین نقاط مختلف روی زمین را فراهم می‌آورد.

مختصات عرض و طول جغرافیایی بر اساس یک بیضی شکل که شکل تقریبی زمین را نشان می‌دهد، اندازه‌گیری می‌شوند.

آنها به ما اجازه می‌دهند تا فواصل و زوایا بین نقاط مختلف روی زمین را اندازه‌گیری کنیم.

2# اهمیت سیستم‌های مختصات در جغرافیا

سیستم‌های مختصات ابزارهای ریاضی هستند که برای تعیین دقیق موقعیت نقاط یا عناصر هندسی در فضا استفاده می‌شوند.

در جغرافیا، این سیستم‌ها امکان نقشه‌برداری دقیق، اندازه‌گیری فواصل و مساحت‌ها و انجام تحلیل‌های مکانی را فراهم می‌آورند.

سیستم مختصات به ما کمک می‌کند تا موقعیت‌های جغرافیایی را با استفاده از مختصات عرض و طول جغرافیایی تعریف کنیم.

این امر پایه و اساس بسیاری از سیستم‌های مرجع فضایی دیگر را تشکیل می‌دهد.

3# مفاهیم پایه‌ای

• درک محورها و صفحات: در این سیستم، محورها خطوطی هستند که نقاط را بر اساس مختصاتشان تعریف می‌کنند.
  در یک سیستم دوبعدی، دو محور (x) و (y) وجود دارند که به صورت عمود بر هم قرار گرفته‌اند و در نقطه‌ای به نام مبدأ با یکدیگر تلاقی می‌کنند.
  این دو محور صفحه‌ای را تشکیل می‌دهند که به چهار بخش یا کوادران تقسیم می‌شود و هر نقطه در این صفحه را می‌توان با استفاده از یک جفت عدد مختصاتی تعریف کرد.
• مفهوم ابعاد: ابعاد در این سیستم‌ها به تعداد محورهایی اشاره دارد که برای تعریف موقعیت یک نقطه در فضا استفاده می‌شوند.
  در یک سیستم دوبعدی، دو محور (x) و (y) برای تعریف موقعیت استفاده می‌شوند.
  در سیستم سه‌بعدی، یک محور اضافی (z) اضافه می‌شود که به صورت عمود بر دو محور دیگر قرار دارد و سه بعد فضایی را تعریف می‌کند.
  این مفهوم را می‌توان به فضاهای با بعد بالاتر نیز گسترش داد، جایی که هر نقطه در فضای (n) بعدی اقلیدسی می‌تواند با استفاده از (n) مختصات کارتزین تعریف شود.

4# انواع سیستم‌های مختصات

انواع مختلف این سیستم‌ها که به طور گسترده در جغرافیا و دیگر علوم مورد استفاده قرار می‌گیرند، عبارت اند از:

• دکارتی (Cartesian Coordinate System): این سیستم از دو یا سه محور متقاطع استفاده می‌کند که هر نقطه را با استفاده از فاصله‌های مشخص شده تا خطوط محور تعریف می‌کند.
• قطبی (Polar Coordinate System): در این سیستم، هر نقطه با استفاده از فاصله شعاعی از یک نقطه مرجع و یک زاویه نسبت به یک خط مرجع تعریف می‌شود.
• استوانه‌ای (Cylindrical Coordinate System): این سیستم یک توسعه سه‌بعدی از سیستم مختصات قطبی است که در آن از یک فاصله شعاعی، یک زاویه و یک ارتفاع برای تعریف موقعیت نقاط استفاده می‌شود.
• کروی (Spherical Coordinate System): سیستمی سه‌بعدی که در آن موقعیت هر نقطه با استفاده از فاصله شعاعی، زاویه قطبی و زاویه آزیموتال تعریف می‌شود.
• مستطیلی (Rectangular Coordinate System): این سیستم مشابه سیستم مختصات دکارتی است ولی بیشتر برای تعریف موقعیت‌ها در فضاهای بزرگتر و پیچیده‌تر استفاده می‌شود.
• سه‌بعدی (3D Coordinate System): سیستمی که از سه محور متقاطع برای تعریف موقعیت نقاط در فضای سه‌بعدی استفاده می‌کند.
• جغرافیایی: این سیستم از عرض و طول جغرافیایی برای تعیین موقعیت نقاط روی سطح زمین استفاده می‌کند و برای ناوبری و نقشه‌برداری جهانی به کار می‌رود.
  عرض جغرافیایی از خط استوا و طول جغرافیایی از نصف‌النهار اولیه گرینویچ اندازه‌گیری می‌شود.

این سیستم‌ها به ما امکان می‌دهند تا موقعیت‌های مکانی را در فضاهای مختلف با دقت بالا تعریف کنیم.

همچنین برای حل مسائل مربوط به نقشه‌برداری، ناوبری، فیزیک و مهندسی از آن‌ها استفاده می‌کنیم.

هر سیستمی بر اساس ویژگی‌های خاص خود برای کاربردهای متفاوتی مناسب است.

1-4# سیستم مختصات دکارتی

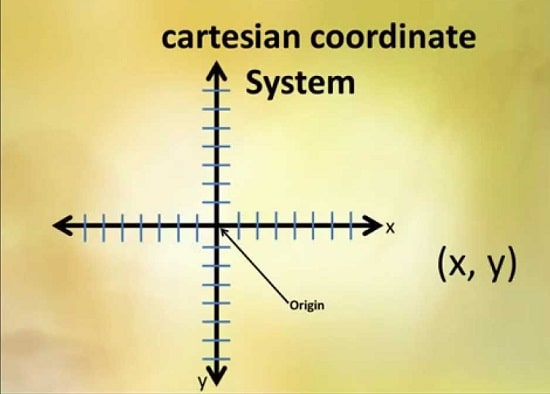
سیستم مختصات دکارتی، که به افتخار ریاضیدان فرانسوی رنه دکارت نامگذاری شده است، یک سیستم مختصات است که در آن هر نقطه در یک صفحه دوبعدی یا فضای سه‌بعدی به طور یکتا با استفاده از یک جفت یا سه‌تایی از اعداد حقیقی تعریف می‌شود.

این اعداد که به عنوان مختصات شناخته می‌شوند، فاصله‌های تعیین شده تا نقطه از دو یا سه خط متقاطع و عمود بر هم هستند که به آن‌ها محورهای مختصات گفته می‌شود.

نقطه‌ای که در آن محورها به هم می‌رسند، مبدأ نامیده می‌شود و دارای مختصات (0, 0) یا (0, 0, 0) است.

• کاربرد سیستم مختصات دکارتی در جغرافیا: در جغرافیا، سیستم مختصات دکارتی می‌تواند برای تعیین موقعیت دقیق نقاط روی نقشه‌های توپوگرافی و GIS استفاده شود.
  این سیستم به جغرافیدانان اجازه می‌دهد تا داده‌های مکانی را با دقت بالا تحلیل کنند و موقعیت‌های جغرافیایی را با استفاده از مختصات X و Y نمایش دهند.
  همچنین، سیستم مختصات دکارتی در مدل‌سازی سه‌بعدی محیط‌های طبیعی و شهری و در تحلیل‌های فضایی که نیاز به دقت مکانی بالا دارند، کاربرد دارد.

2-4# سیستم مختصات قطبی

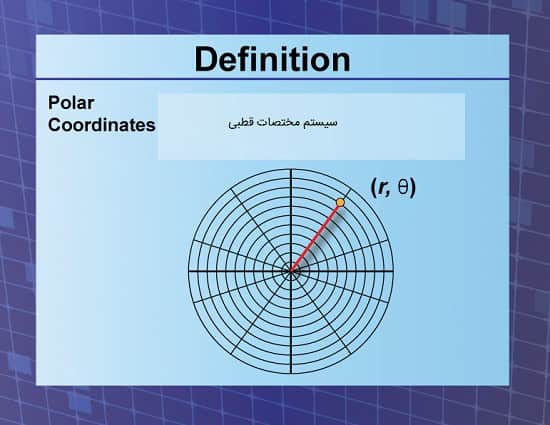
سیستم مختصات قطبی یک سیستم دوبعدی است که در آن هر نقطه بر روی صفحه با استفاده از فاصله از یک نقطه مرجع و یک زاویه از یک جهت مرجع تعیین می‌شود.

نقطه مرجع، مشابه مبدأ در سیستم مختصات دکارتی، قطب نامیده می‌شود و پرتویی که از قطب در جهت مرجع حرکت می‌کند، محور قطبی است.

فاصله از قطب، مختصه شعاعی یا فاصله شعاعی و زاویه، مختصه زاویه‌ای، زاویه قطبی یا آزیموت نامیده می‌شود.

• کاربرد سیستم مختصات قطبی در جغرافیا: این سیستم قطبی برای مطالعه حرکت دایره‌ای و مداری و در مواردی که پدیده مورد بررسی به طور ذاتی به جهت و طول از یک نقطه مرکزی در یک صفحه مرتبط است، مانند مارپیچ‌ها، مناسب است.
  در جغرافیا، این سیستم می‌تواند برای تعیین موقعیت‌های دقیق بر روی زمین استفاده شود، جایی که عرض و طول جغرافیایی می‌توانند به عنوان نوعی از مختصات قطبی در نظر گرفته شوند.
  همچنین در ناوبری، به ویژه دریانوردی و هوانوردی، جهت‌ها برای نشان دادن مسیر با استفاده از مختصات قطبی اندازه‌گیری می‌شوند.

3-4# سیستم مختصات استوانه‌ای

سیستم مختصات استوانه‌ای یک سیستم سه‌بعدی است که موقعیت هر نقطه در فضا را با استفاده از سه مختصه تعیین می‌کند: فاصله شعاعی از محور مرجع، زاویه نسبت به جهت مرجع و ارتفاع از یک صفحه مرجع.

این سیستم برای شناسایی و توصیف موقعیت‌هایی که در رابطه با اشیا یا پدیده‌هایی با تقارن دورانی حول یک محور طولی هستند، مانند جریان آب در لوله‌های دایره‌ای یا توزیع حرارت در یک استوانه، مفید است.

• کاربرد سیستم مختصات استوانه‌ای در جغرافیا: در جغرافیا، سیستم مختصات استوانه‌ای به ویژه در نقشه‌برداری و کارتوگرافی کاربرد دارد.
  این سیستم در پروژه‌های نقشه‌برداری استوانه‌ای مانند پروژه مرکاتور و پروژه مرکاتور عرضی استفاده می‌شود که برای نقشه‌هایی با تمرکز بر مناطقی که بیشتر در جهت شمال-جنوب گسترش یافته‌اند، مناسب است.
  این سیستم همچنین در سیستم‌های دولتی (State Plane Coordinate System) به کار می‌رود که برای نقشه‌برداری دقیق مناطق خاصی از زمین طراحی شده‌اند.

4-4# سیستم مختصات کروی

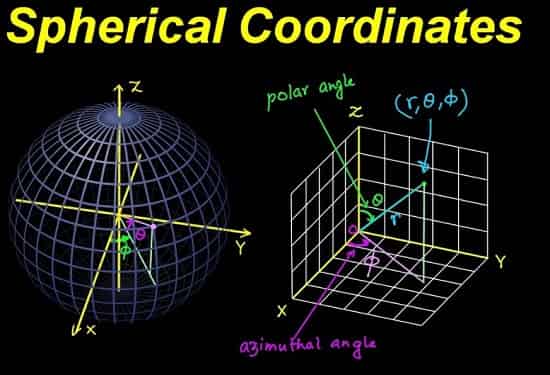
سیستم مختصات کروی یک سیستم سه‌بعدی است که در آن موقعیت هر نقطه در فضا با استفاده از سه مختصه تعیین می‌شود: فاصله شعاعی (r)، زاویه قطبی (\theta)، و زاویه آزیموتال (\phi).

فاصله شعاعی از نقطه مبدأ، زاویه قطبی بین محور (z) و خط شعاعی و زاویه آزیموتال بین پروجکشن خط شعاعی بر روی صفحه مرجع (xy) و یکی از محورهای (x) یا (y) اندازه‌گیری می‌شود.

این سیستم برای توصیف موقعیت‌هایی که در رابطه با سطوح کروی قرار دارند، مانند سیارات، ستارگان و سایر اجرام آسمانی، استفاده می‌شود.

• کاربرد سیستم مختصات کروی در جغرافیا: در جغرافیا، سیستم مختصات کروی برای تعیین موقعیت‌های دقیق بر روی زمین استفاده می‌شود، جایی که عرض و طول جغرافیایی می‌توانند به عنوان نوعی از مختصات کروی در نظر گرفته شوند.
  این سیستم به ویژه برای تعیین موقعیت‌های جغرافیایی بر روی زمین به عنوان عرض و طول جغرافیایی استفاده می‌شود.
  همچنین پایه و اساس بسیاری از سیستم‌های مرجع فضایی دیگر را تشکیل می‌دهد.
  این سیستم در ناوبری دریایی و هوایی که در آن جهت‌ها برای نشان دادن مسیر با استفاده از مختصات کروی اندازه‌گیری می‌شوند، کاربرد دارد.

5-4# سیستم مختصات مستطیلی

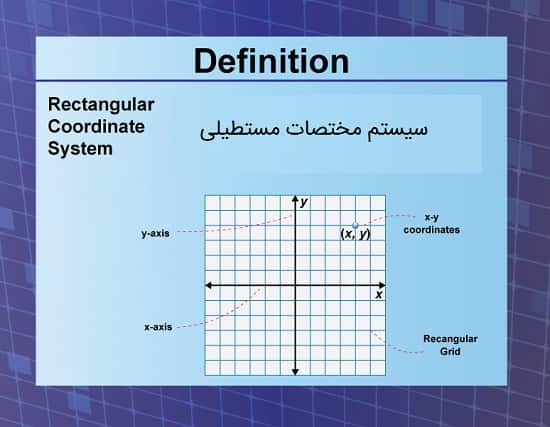
سیستم مختصات مستطیلی، که اغلب به عنوان سیستم مختصات دکارتی شناخته می‌شود، بر اساس یک صفحه دوبعدی است که از دو محور عمود بر هم تشکیل شده است: محور (x) و محور (y).

این محورها صفحه را به چهار بخش یا کوادران تقسیم می‌کنند و هر نقطه در صفحه می‌تواند با استفاده از یک جفت عدد مختصاتی (x, y) تعریف شود.

این سیستم برای ترسیم نمودارهای دوبعدی و تحلیل روابط بین دو متغیر استفاده می‌شود و در ریاضیات، فیزیک و مهندسی کاربردهای فراوانی دارد.

• کاربرد سیستم مختصات مستطیلی در جغرافیا: در جغرافیا، سیستم مختصات مستطیلی می‌تواند برای تحلیل داده‌های مکانی در یک صفحه دوبعدی مورد استفاده قرار گیرد.
  این سیستم به ویژه در GIS (سیستم‌های اطلاعات جغرافیایی) کاربرد دارد، جایی که داده‌های مکانی بر روی یک صفحه دوبعدی نمایش داده می‌شوند.
  همچنین برای تحلیل‌های فضایی مانند تعیین مساحت، محاسبه فواصل و ترسیم نمودارهای مکانی استفاده می‌شود.
  این سیستم در کارتوگرافی برای ترسیم نقشه‌های دقیق و مدل‌سازی فضایی به کار می‌رود و امکان تحلیل پیچیده‌تر داده‌های جغرافیایی را فراهم می‌آورد.

6-4# سیستم مختصات سه‌بعدی

سیستم مختصات سه‌بعدی یک روش ریاضیاتی است که برای نمایش سه بعد (3D) در یک فرمت دو بعدی (2D) با استفاده از سه مقدار شناخته شده به عنوان X ،Y و Z به کار می‌رود.

این سیستم به سیستم‌های اطلاعات جغرافیایی (GIS) اجازه می‌دهد تا جهان را در مکان‌های خاص نقشه‌برداری کنند، فواصل و مساحت‌ها را اندازه‌گیری کنند و تحلیل‌های فضایی انجام دهند.

• کاربرد سیستم مختصات سه‌بعدی در جغرافیا: در جغرافیا، سیستم مختصات سه‌بعدی برای مدل‌سازی و تحلیل محیط‌های طبیعی و ساخته شده به کار می‌رود.
  این سیستم امکان می‌دهد تا پدیده‌های جغرافیایی مانند تپه‌ها، دره‌ها و ساختمان‌ها را با دقت بالا در سه بعد نمایش دهیم.
  همچنین در GIS برای ایجاد نقشه‌های سه‌بعدی که می‌توانند توپوگرافی، اقلیم و سایر ویژگی‌های محیطی را با جزئیات بیشتر نشان دهند، استفاده می‌شود.
  این سیستم همچنین در برنامه‌ریزی شهری و مدیریت منابع طبیعی برای تحلیل تأثیرات سه‌بعدی و برنامه‌ریزی فضایی مورد استفاده قرار می‌گیرد.

7-4# سیستم مختصات جغرافیایی

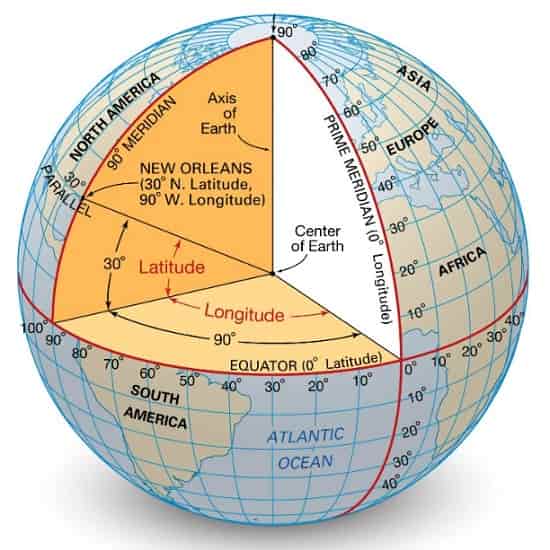
سیستم مختصات جغرافیایی یک سیستم مختصات کروی یا ژئودتیک است که برای اندازه‌گیری و ارتباط دادن موقعیت‌ها مستقیماً روی زمین به عنوان عرض و طول جغرافیایی استفاده می‌شود.

این سیستم ساده‌ترین، قدیمی‌ترین و پرکاربردترین سیستم‌های مرجع فضایی است که در حال حاضر مورد استفاده قرار می‌گیرد و پایه و اساس بیشتر سیستم‌های دیگر را تشکیل می‌دهد.

• توضیح عرض و طول جغرافیایی: عرض جغرافیایی موقعیت شمالی یا جنوبی یک نقطه روی زمین را تعیین می‌کند، در حالی که طول جغرافیایی موقعیت شرقی یا غربی آن را مشخص می‌کند.
  خطوط عرض جغرافیایی موازی یکدیگر و افقی هستند، در حالی که خطوط طول جغرافیایی عمودی اند و در قطب‌ها به هم می‌رسند.
• نقش در سیستم‌های موقعیت‌یاب جهانی (GPS): این سیستم جغرافیایی نقش مهمی در سیستم‌های موقعیت‌یاب جهانی (GPS) دارد.
  GPS از سیستم مختصات جهانی ژئودتیک (WGS84) به عنوان سیستم مختصات مرجع خود استفاده می‌کند.
  این سیستم شامل یک بیضی شکل مرجع، یک سیستم مختصات استاندارد، داده‌های ارتفاع و یک ژئوئید است.
  GPS با استفاده از این سیستم مختصات، موقعیت سه‌بعدی و زمان دقیق را برای کاربران فراهم می‌آورد.

5# تبدیل بین مختصات دکارتی و قطبی

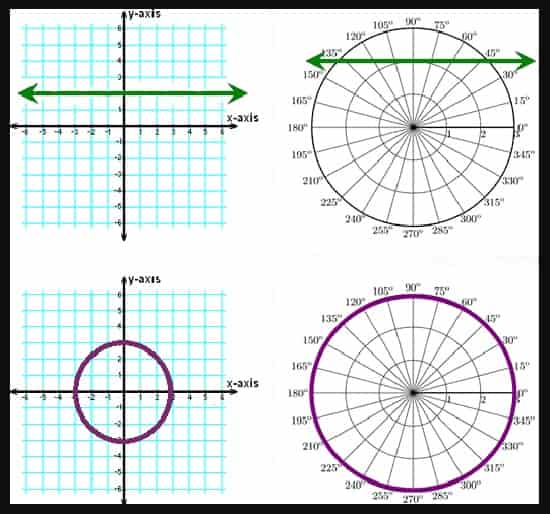
برای تبدیل از مختصات قطبی به مختصات دکارتی، دو مختصه در سیستم قطبی (فاصله و زاویه) را می‌گیریم و از مجموعه قوانین زیر استفاده می‌کنیم:

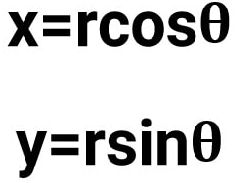
برای تبدیل از مختصات دکارتی به مختصات قطبی، مختصات نقطه در مختصات دکارتی (x,y) را می‌گیریم و از فرمول‌های زیر استفاده می‌کنیم:

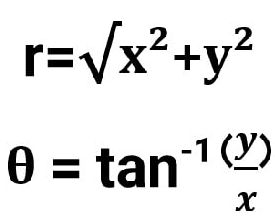
این تبدیلات از مفاهیم دایره مثلثاتی مستقیماً می‌آیند و برای پوشش کل صفحه به طور مناسب گسترده یا کوچک می‌شوند.

6# تبدیل سیستم مختصات استوانه‌ای به سایر سیستم‌های مختصات

تبدیل از مختصات استوانه‌ای به مختصات دکارتی با استفاده از روابط زیر انجام می‌شود:

و برای تبدیل از مختصات دکارتی به مختصات استوانه‌ای، می‌توان از فرمول‌های زیر استفاده کرد:

این تبدیلات به ما امکان می‌دهند تا موقعیت نقاط را بین سیستم‌های مختصات مختلف به راحتی تغییر دهیم.

همچنین برای حل مسائل مهندسی و فیزیکی که در آن‌ها استفاده از یک سیستم خاص مفیدتر است، می‌توانیم از آنها استفاده کنیم.

جمع بندی

سیستم مختصات برای توصیف دقیق موقعیت اشیا یا ویژگی‌ها در فضا ضروری است.

آن‌ها در GIS برای انجام تحلیل‌های مکانی، مانند اندازه‌گیری فواصل، محاسبه مساحت‌ها و انجام عملیات هندسی بر روی داده‌های مکانی استفاده می‌شوند.

این سیستم‌ها به عنوان چارچوب مرجع برای شناسایی موقعیت نقطه‌ای بر روی سطح زمین عمل می‌کنند.

همچنین امکان استفاده از موقعیت‌های مشترک برای ادغام داده‌های جغرافیایی را فراهم می‌آورند که تجزیه و تحلیل و تصویرسازی داده‌ها را آسان‌تر می‌کند.

نظرتون درباره این مقاله چیه؟
ما رو راهنمایی کنید تا اون رو کامل تر کنیم و نواقصش رو رفع کنیم.
توی بخش دیدگاه ها منتظر پیشنهادهای فوق العاده شما هستیم.